题目内容
【题目】已知点O(0,0),B(1,2).
(1)若点A在y轴的正半轴上,且三角形OAB的面积为2,求点A的坐标.
(2)若点A(3,0),BC∥OA,BC=OA,求点C的坐标.
(3)若点A(3,0),点D(3,﹣4),求四边形ODAB的面积.
【答案】
(1)解:∵点A在y轴的正半轴上,
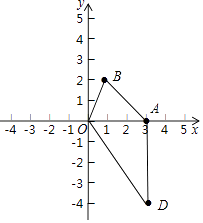
设A(0,m),
∵三角形OAB的面积为2,
∴ ![]() m×1=2,
m×1=2,
∴m=4,
∴A(0,4);
(2)解:∵A(3,0),
∴OA=3,
∵BC∥OA,BC=OA,B(1,2),
∴C(4,2)或(﹣2,2);
(3)解:四边形ODAB的面积=S△ABO+S△OAD= ![]() 3×2+
3×2+ ![]() 3×4=9.
3×4=9.
【解析】C点可在B左侧或右侧两种情况;四边形面积采用求和的方法.
【考点精析】利用三角形的面积对题目进行判断即可得到答案,需要熟知三角形的面积=1/2×底×高.

练习册系列答案
相关题目
【题目】农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为