题目内容
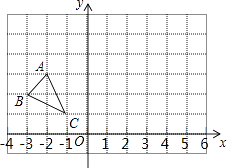
【题目】已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
△ABC | A（a，0） | B（3，0） | C（5，5） |
△A′B′C′ | A′（4，2） | B′（7，b） | C′（c，7） |
（1）观察表中各对应点坐标的变化，并填空：a= ， b= ， c=；
（2）在平面直角坐标系中画出△ABC及平移后的△A′B′C′；
（3）直接写出△A′B′C′的面积是 ．
【答案】
（1）0,2,9
（2）解：如图所示
（3）
【解析】（1）由表格得出：
∵利用对应点坐标特点：A（a，0），A′（4，2）；B（3，0），B′（7，b）；C（5，5），C′（c，7）
∴横坐标加4，纵坐标加2，
∴a=0，b=2，c=9．
所以答案是：0，2，9；
（ 2 ）平移后，如图所示．
（ 3 ）△A′B′C′的面积为： 
×3×5= ．
所以答案是： ．
【考点精析】解答此题的关键在于理解坐标与图形变化-平移的相关知识，掌握新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
