题目内容
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.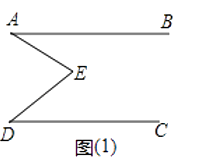
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
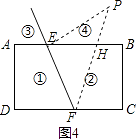
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)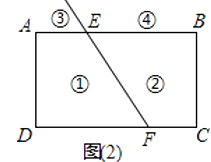
【答案】
(1)解:①如图①,过点E作EF∥AB,
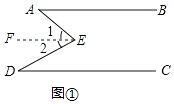
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=30°,∠D=40°,
∴∠1=∠A=30°,∠2=∠D=40°,
∴∠AED=∠1+∠2=70°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=20°,∠D=60°,
∴∠1=∠A=20°,∠2=∠D=60°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC,
∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)解:点P在区域①时,
如图1,在五边形EBCFP中,∠PEB+∠B+∠C+∠PFC+∠P=540°
∴∠EPF=540°﹣∠B﹣∠C﹣(∠PEB+∠PFC)=360°﹣(∠PEB+∠PFC);
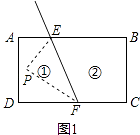
点P在区域②时,如图2,同(1)的方法得,∠EPF=∠PEB+∠PFC;
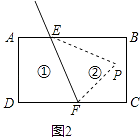
点P在区域③时,如图3,同(1)的方法得,∠EPF=∠PEB﹣∠PFC;

点P在区域④时,如图4,同(1)的方法得,∠EPF=∠PFC﹣∠PEB.
【解析】解阶梯式问题的基本策略是利用第1问的结论,特殊问题的方法可运用到一般问题中.

【题目】农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
实验的麦种数/粒 | 500 | 500 | 500 | 500 | 500 |
发芽的麦种数/粒 | 492 | 487 | 491 | 493 | 489 |
发芽率/% | 98.40 | 97.40 | 98.20 | 98.60 | 97.80 |
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为