题目内容
已知：如图，AB是⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足是D．
求证：AC平分∠DAB．
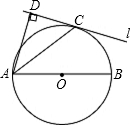
求证：AC平分∠DAB．
连接OC，
∵直线l与⊙O相切于点C，
∴OC⊥CD；
又∵AD⊥CD，
∴AD∥OC，
∴∠DAC=∠ACO；
又∵OA=OC，
∴∠ACO=∠CAO，
∴∠DAC=∠CAO，
即AC平分∠DAB．
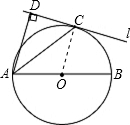
∵直线l与⊙O相切于点C，
∴OC⊥CD；
又∵AD⊥CD，
∴AD∥OC，
∴∠DAC=∠ACO；
又∵OA=OC，
∴∠ACO=∠CAO，
∴∠DAC=∠CAO，
即AC平分∠DAB．
练习册系列答案
相关题目
限，点C的坐标为（0，-2），过B点作BE⊥CD于点E．
