题目内容
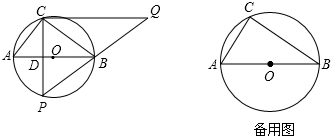
如图，AB是⊙O的直径，AC和BD是它的两条切线，CO平分∠ACD．
（1）求证：CD是⊙O的切线；
（2）若AC=2，BD=3，求AB的长．
（1）求证：CD是⊙O的切线；
（2）若AC=2，BD=3，求AB的长．
（1）证明：过O点作OE⊥CD，垂足为E，
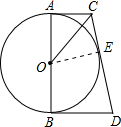
∵AC是⊙O的切线，
∴OA⊥AC，
∵CO平分∠ACD，OE⊥CD，
∴OA=OE，
∴CD是⊙O的切线．
（2）过C点作CF⊥BD，垂足为F，
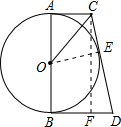
∵AC，CD，BD都是⊙O的切线，
∴AC=CE=2，BD=DE=3，
∴CD=CE+DE=5，
∵∠CAB=∠ABD=∠CFB=90°，
∴四边形ABFC是矩形，
∴BF=AC=2，DF=BD-BF=1，
在Rt△CDF中，CF2=CD2-DF2=52-12=24，
∴AB=CF=2
．
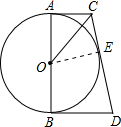
∵AC是⊙O的切线，
∴OA⊥AC，
∵CO平分∠ACD，OE⊥CD，
∴OA=OE，
∴CD是⊙O的切线．
（2）过C点作CF⊥BD，垂足为F，
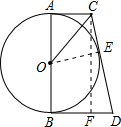
∵AC，CD，BD都是⊙O的切线，
∴AC=CE=2，BD=DE=3，
∴CD=CE+DE=5，
∵∠CAB=∠ABD=∠CFB=90°，
∴四边形ABFC是矩形，
∴BF=AC=2，DF=BD-BF=1，
在Rt△CDF中，CF2=CD2-DF2=52-12=24，
∴AB=CF=2
| 6 |
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
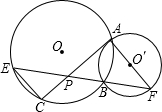与AC相交于点P．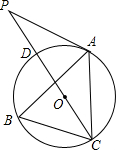
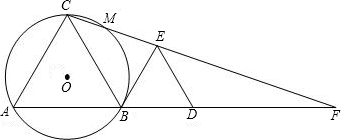
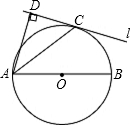
点P，tan∠CAB=