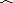题目内容
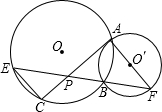
如图,PA、PB分别切⊙O于A、B,AC是⊙O的直径,过P作PM⊥BP交CB的延长线于M
(1)求证:∠C=∠M
(2)若cos∠C=
,CM=3,求⊙O的半径.

(1)求证:∠C=∠M
(2)若cos∠C=
| 2 |
| 3 |

(1)证明,如图,连接OB、OP.∵PB是⊙O的切线,点B是切点,
∴∠PBO=90°.
又∵PM⊥BP,
∴∠BPM=90°,
∴∠PBO=∠BPM,
∴MP∥OB,
∴∠M=∠OBC,
∵OB=OC,
∴∠OBC=∠C,
∴∠C=∠M;
(2)如图,连接AB,则OP⊥AB,CB⊥AB.
∴OP∥CM.
又∵MP∥OB,
∴四边形OBMP是平行四边形.
设⊙O的半径为R,则MP=OB=R.
∵cos∠C=
=
,
∴BC=
R.
∴cos∠M=cos∠C=
=
,
∴BM=
R,
∴
R+
R=3,
解得,R=
.

∴∠PBO=90°.
又∵PM⊥BP,
∴∠BPM=90°,
∴∠PBO=∠BPM,
∴MP∥OB,
∴∠M=∠OBC,
∵OB=OC,
∴∠OBC=∠C,
∴∠C=∠M;
(2)如图,连接AB,则OP⊥AB,CB⊥AB.
∴OP∥CM.
又∵MP∥OB,
∴四边形OBMP是平行四边形.
设⊙O的半径为R,则MP=OB=R.
∵cos∠C=
| BC |
| AC |
| 2 |
| 3 |
∴BC=
| 4 |
| 3 |
∴cos∠M=cos∠C=
| PM |
| BM |
| 2 |
| 3 |
∴BM=
| 3 |
| 2 |
∴
| 4 |
| 3 |
| 3 |
| 2 |
解得,R=
| 18 |
| 17 |


练习册系列答案
相关题目
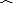

 与AC相交于点P.
与AC相交于点P.