题目内容
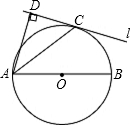
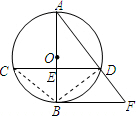
已知:如图,⊙O的直径AB与弦CD相交于E,
=
,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF.
(2)连接BC,若⊙O的半径为4,cos∠BCD=
,求线段AD、CD的长.

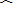 |
| BC |
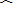 |
| BD |
(1)求证:CD∥BF.
(2)连接BC,若⊙O的半径为4,cos∠BCD=
| 3 |
| 4 |

(1)证明:∵直径AB平分
,
∴AB⊥CD.
∵BF与⊙O相切,AB是⊙O的直径,
∴AB⊥BF.
∴CD∥BF.
(2)连接BD,BC.
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ADB中,
∵cos∠BAF=cos∠BCD=
,AB=4×2=8.
∴AD=AB•cos∠BAF=8×
=6.
∵AB⊥CD于E,
在Rt△AED中,cos∠BAF=cos∠BCD=
,sin∠BAF=
.
∴DE=AD•sin∠BAF=6×
=
.
∵直径AB平分
,
∴CD=2DE=3
.
 |
| CD |
∴AB⊥CD.
∵BF与⊙O相切,AB是⊙O的直径,
∴AB⊥BF.
∴CD∥BF.
(2)连接BD,BC.
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ADB中,
∵cos∠BAF=cos∠BCD=
| 3 |
| 4 |
∴AD=AB•cos∠BAF=8×
| 3 |
| 4 |
∵AB⊥CD于E,
在Rt△AED中,cos∠BAF=cos∠BCD=
| 3 |
| 4 |
| ||
| 4 |
∴DE=AD•sin∠BAF=6×
| ||
| 4 |
| 3 |
| 2 |
| 7 |
∵直径AB平分
 |
| CD |
∴CD=2DE=3
| 7 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目