题目内容
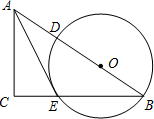
如图，P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，BC∥OP且交⊙O于点C，请准确判断直线PC与⊙O是怎样的位置关系，并说明理由．
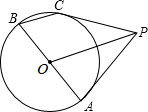
PC与⊙O相切．理由如下：
连接OC，
∵OC=OB，
∴∠B=∠OCB，
∵BC∥OP，
∴∠B=∠AOP，∠OCB=∠COP，
∴∠AOP=∠COP，
在△AOP与△COP中
，
∴△AOP≌△COP（SAS），
又∵PA是⊙O的切线，
∴OA⊥PA，
∴∠OAP=90°，
∴∠OCP=90°，
∴OC⊥PC．
∴PC是⊙O的切线．
连接OC，
∵OC=OB，
∴∠B=∠OCB，
∵BC∥OP，
∴∠B=∠AOP，∠OCB=∠COP，
∴∠AOP=∠COP，
在△AOP与△COP中
|
∴△AOP≌△COP（SAS），
又∵PA是⊙O的切线，
∴OA⊥PA，
∴∠OAP=90°，
∴∠OCP=90°，
∴OC⊥PC．
∴PC是⊙O的切线．
练习册系列答案
相关题目
