题目内容
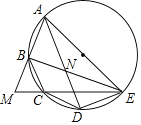
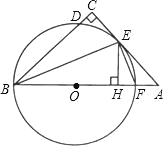
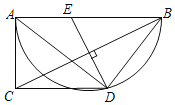
【题目】如图,AB为半圆的直径,点D在半圆弧上,过点D作AB的平行线与过点A半圆的切线交于点C,点E在AB上,若DE垂直平分BC,则![]() =______.
=______.
【答案】![]()
【解析】
连接CE,过点B作BH⊥CD交CD的延长线于点H,可证四边形ACHB是矩形,可得AC=BH,AB=CH,由垂直平分线的性质可得BE=CE,CD=BD,可证CE=BE=CD=DB,通过证明Rt△ACE≌Rt△HBD,可得AE=DH,通过证明△ACD∽△DHB,可得AC2=AEBE,由勾股定理可得BE2﹣AE2=AC2,可得关于BE,AE的方程,即可求解.
解:连接CE,过点B作BH⊥CD交CD的延长线于点H,
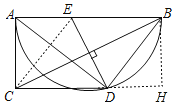
∵AC是半圆的切线
∴AC⊥AB,
∵CD∥AB,
∴AC⊥CD,且BH⊥CD,AC⊥AB,
∴四边形ACHB是矩形,
∴AC=BH,AB=CH,
∵DE垂直平分BC,
∴BE=CE,CD=BD,且DE⊥BC,
∴∠BED=∠CED,
∵AB∥CD,
∴∠BED=∠CDE=∠CED,
∴CE=CD,
∴CE=BE=CD=DB,
∵AC=BH,CE=BD,
∴Rt△ACE≌Rt△HBD(HL)
∴AE=DH,
∵CE2﹣AE2=AC2,
∴BE2﹣AE2=AC2,
∵AB是直径,
∴∠ADB=90°,
∴∠ADC+∠BDH=90°,且∠ADC+∠CAD=90°,
∴∠CAD=∠BDH,且∠ACD=∠BHD,
∴△ACD∽△DHB,
∴![]() ,
,
∴AC2=AEBE,
∴BE2﹣AE2=AEBE,
∴BE=![]() AE,
AE,
∴![]()
故答案为:![]() .
.

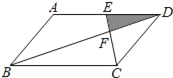
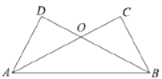
【题目】在证明“已知:如图,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .”时,两位同学的证法如下:
.”时,两位同学的证法如下:
证法一:由勾股定理,得
|
证法二:
|
(1)反思:上述两位同学的证法中,有一位同学已完成的证明部分有一处错误,请把错误序号写出.
(2)请你选择其中一种证法,完成证明.