题目内容
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
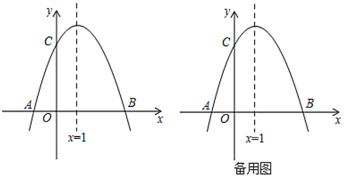
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
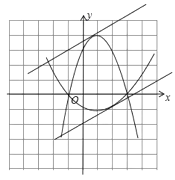
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
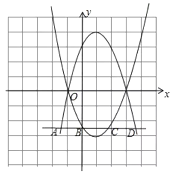
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
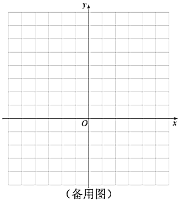
【答案】(1)![]() ,
,![]() ;
;![]() ;(2)①
;(2)①![]() ,
,![]() ;
;![]() ;对称轴为直线
;对称轴为直线![]() (或与
(或与![]() 轴交点为
轴交点为![]() ,
,![]() );②
);②![]() ,且
,且![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据![]() ,可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,本题得以解决;
,可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,本题得以解决;
(2)①将n=1,代入yn得![]() ,据此可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,然后根据(1)中的结果,写出抛物线y,yn的一条相同的图象性质即可;
,据此可以求得该抛物线与x轴的交点和该抛物线的顶点坐标,然后根据(1)中的结果,写出抛物线y,yn的一条相同的图象性质即可;
②求出直线![]() 与
与![]() 相交只有1个交点时m的值,直线
相交只有1个交点时m的值,直线![]() 与
与![]() 相交只有1个交点时m的值,
相交只有1个交点时m的值,![]() 过点
过点![]() 时m的值,
时m的值,![]() 过点
过点![]() 时m的值,根据函数图象,从而可以得到当直线y=
时m的值,根据函数图象,从而可以得到当直线y=![]() x+m与y,yn相交共有4个交点时,m的取值范围;
x+m与y,yn相交共有4个交点时,m的取值范围;
(3)根据一元二次方程根与系数的关系求出![]() ,
,![]() ,根据
,根据![]() 可得
可得![]() ,进而可以求出k,n之间满足的关系式.
,进而可以求出k,n之间满足的关系式.
解:(1)∵抛物线![]() ,
,
∴当y=0时,x1=3,x2=1,该抛物线的顶点坐标为(1,4),
∴抛物线y=x2+2x+3与x轴的交点为(3,0),(1,0),
故答案为:(1,0),(3,0);(1,4);
(2)①当n=1时,
抛物线![]() ,
,
∴当y1=0时,x3=3,x4=1,该抛物线的顶点坐标为(1,![]() ),
),
∴该抛物线与x轴的交点为(3,0),(1,0),
抛物线y,yn的一条相同的图象性质是对称轴都是x=1(或与x轴的交点都是(1,0),(3,0));
②当直线![]() 与
与![]() 相交只有1个交点时,
相交只有1个交点时,
由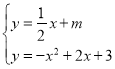 ,得
,得![]() ,
,
则![]() ,
,
∴![]() ,
,
当直线![]() 与
与![]() 相交只有1个交点时,
相交只有1个交点时,
由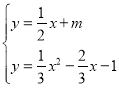 ,得
,得![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.
把![]() ,代入
,代入![]() ,得
,得![]() ;把
;把![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ;
;
(3)由![]() ,得
,得![]() ,
,
∴![]() ,
,
由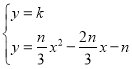 ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
化简得:![]() .
.

 名师指导期末冲刺卷系列答案
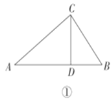
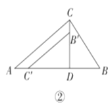
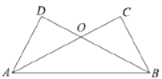
名师指导期末冲刺卷系列答案【题目】在证明“已知:如图,![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .”时,两位同学的证法如下:
.”时,两位同学的证法如下:
证法一:由勾股定理,得
|
证法二:
|
(1)反思:上述两位同学的证法中,有一位同学已完成的证明部分有一处错误,请把错误序号写出.
(2)请你选择其中一种证法,完成证明.
【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?