题目内容
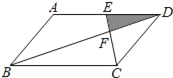
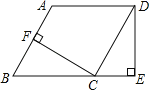
【题目】如图，在ABCD中，CF⊥AB于点F，过点D作DE⊥BC的延长线于点E，且CF＝DE．
（1）求证：△BFC≌△CED；
（2）若∠B＝60°，AF＝5，求BC的长．
【答案】（1）详见解析；（2）BC＝10．
【解析】
（1）由平行四边形的性质可得AB∥CD，可得∠B＝∠DCE，由“AAS”可证△BFC≌△CED；
（2）设BC＝CD＝AB＝x，由直角三角形的性质可得（x﹣5）＝
x，可求x的值，即可求BC的长．
（1）证明：∵四边形ABCD是平行四边形
∴AB∥CD，AB＝CD
∴∠B＝∠DCE
∵CF⊥AB，DE⊥BC，
∴∠CFB＝∠DEC＝90°，且CF＝DE，∠B＝∠DCE
∴△BFC≌△CED （AAS）
（2）∵△BFC≌△CED
∴BC＝DC＝AB
设BC＝x，
∴CD＝AB＝x
在Rt△BCF中，∠B＝60°
∴∠BCF＝30°
∴FB＝BC
∴（x﹣5）＝x
解得x＝10
∴BC＝10．
练习册系列答案
相关题目
【题目】2018年某省实施人才引进政策，对引进人才给予资金扶持和落户优惠，海内外英才纷纷向组织部门递交报名表．为了了解报名人员年龄结构情况，抽样调查了50名报名人员的年龄（单位：岁），将抽样得到的数据分成5组，统计如下表：
分组 | 频数（人数） | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
（1）请将表格中空格填写完整；
（2）样本数据的中位数落在_____，若把样本数据制成扇形统计图，则“大于30岁不大于40岁”的圆心角为______度；
（3）如果共有2000人报名，请你根据上面数据，估计年龄不大于40岁的报名人员会有多少人？
