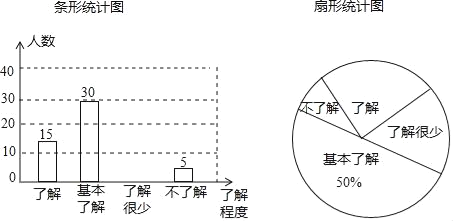
题目内容
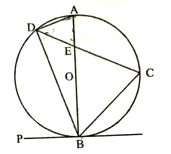
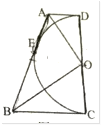
【题目】如图,已知半圆![]() 与四边形
与四边形![]() 的边
的边![]() 都相切,切点分别为
都相切,切点分别为![]() ,半径
,半径![]() ,则
,则![]() ___________.
___________.
【答案】1
【解析】
连接 OE,由切线长定理可得∠AOE=![]() ∠DOE,∠BOE=
∠DOE,∠BOE=![]() ∠EOC,再根据∠DOE+∠EOC=180°,可得∠AOB=90°,继而可证△AEO∽△OEB,根据相似三角形对应边成比例即可得.
∠EOC,再根据∠DOE+∠EOC=180°,可得∠AOB=90°,继而可证△AEO∽△OEB,根据相似三角形对应边成比例即可得.
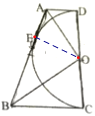
如图,连接 OE,
∵AD、AB与半圆 O 相切,
∴ OE⊥AB,OA平分∠DOE,
∴∠AOE=![]() ∠DOE,
∠DOE,
同理∠BOE=![]() ∠EOC,
∠EOC,
∵∠DOE+∠EOC=180°,
∴∠AOE+∠BOE=90°,
即∠AOB=90°,
∴∠ABO+∠BAO=90°,∵∠BAO+∠AOE=90°,
∴∠ABO=∠AOE,
∵∠OEA=∠BEO=90°,
∴△AEO∽△OEB,
∴AE:OE=OE:BE,
∴AEBE=OE=1,
故答案为:1.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目