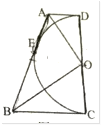
题目内容
【题目】如图, ![]() 是以
是以![]() 为直径的
为直径的![]() 上的点,
上的点,![]() ,弦
,弦![]() 交
交![]() 于点
于点![]() .
.
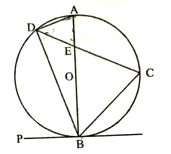
(1)当![]() 是
是![]() 的切线时,求证:
的切线时,求证: ![]() ;
;
(2)求证: ![]() ;
;
(3)已知![]() ,
,![]() 是半径
是半径![]() 的中点,求线段
的中点,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)DE=![]()
【解析】(1)由AB是直径,可得∠DAB+∠ABD=90°,再根据 PB是⊙O的切线,可得∠ABD+∠PBD=90°,根据同角的余角相等即可证得∠PBD=∠DAB;
(2)证明△BCE∽△DCB,根据相似三角形对应边成比例可得BC2=CECD,再根据CD=CE+DE经过推导即可得BC2- CE2= CEDE;
(3) 连接OC,由![]() ,AB是直径,可得∠AOC=∠BOC=90°,根据勾股定理则有CE=OE+CO, BC=OB+CO ,再根据OA=4 ,E 是半径 OA 的中点,继而可得BC=4
,AB是直径,可得∠AOC=∠BOC=90°,根据勾股定理则有CE=OE+CO, BC=OB+CO ,再根据OA=4 ,E 是半径 OA 的中点,继而可得BC=4![]() ,CE=2
,CE=2![]() ,再根据(2)中 BC-CE=CE·DE,即可求得DE的长.
,再根据(2)中 BC-CE=CE·DE,即可求得DE的长.
(1)∵AB是直径,
∴∠ADB=90°,即∠DAB+∠ABD=90°,
又 ∵ PB是⊙O的切线,
∴PB⊥AB,
∴∠ABP=90°,即∠ABD+∠PBD=90°,
∴∠PBD=∠DAB;
(2)∵![]() ,
,
∴∠BDC=∠EBC,
又∵∠BCE=BCD,
∴△BCE∽△DCB,
∴BC:CE=CD:BC,
∴BC2=CECD,
∴BC2=CE(CE+DE),
∴BC2=CE2+CEDE,
∴BC2- CE2= CEDE;
(3)如图,连接OC,
∵![]() ,AB是直径,
,AB是直径,
∴∠AOC=∠BOC=90°,
∴CE=OE+CO, BC=OB+CO ,
∵OA=4 ,E 是半径 OA 的中点,
∴BC=4![]() ,CE=2
,CE=2![]() ,
,
由(2)中 BC-CE=CE·DE,所以 DE=(BC-CE)÷CE=12÷2![]() =
= ![]() ,
,
故 DE=![]() .
.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:克) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(3)若该种食品的合格标准为450±5克,求该食品的抽样检测的合格率.