题目内容
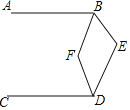
【题目】矩形(非正方形)四个内角的平分线围成的四边形是__________形.(埴特殊四边形)
【答案】正方
【解析】
此类题根据矩形性质,三角形内角和定理及角平分线定义得到所求的四边形的各个角为90°,进而求解.
∵AF,BE是矩形的内角平分线.
∴∠ABF=∠BAF-90°.
故∠1=∠2=90°.
同理可证四边形GMON四个内角都是90°,则四边形GMON为矩形.
又∵有矩形ABCD且AF、BE、DK、CJ为矩形ABCD四角的平分线,
∴有等腰直角△DOC,等腰直角△AMD,等腰直角△BNC,AD=BC.
∴OD=OC,△AMD≌△BNC,
∴NC=DM,
∴NC-OC=DM-OD,
即OM=ON,
∴矩形GMON为正方形,
故答案为正方.


练习册系列答案
相关题目