题目内容
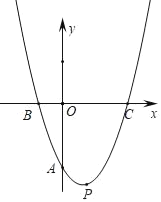
【题目】如图,菱形ABCD顶点A在函数y=![]() (x>0)的图像上,函数y=
(x>0)的图像上,函数y=![]() (k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
(k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
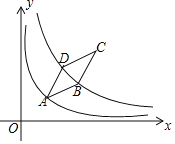
【答案】![]()
【解析】
连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,得O、A、C在第一象限的角平分线上,求得A点坐标,进而求得D点坐标,便可求得结果.
连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,
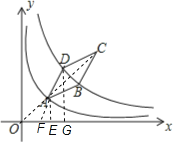
∵函数y=![]() (k>4,x>0)的图象关于直线AC对称,
(k>4,x>0)的图象关于直线AC对称,
∴O,A,C三点在同直线上,且∠COE=45°,
∴OE=AE,
不妨设OE=AE=a,则A(a,a),
∵点A在在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴a2=4,
∴a=±2(负值舍去),
∴a=2,
∴AE=OE=2,
∵四边形ABCD是菱形,∠ADC=150°,
∴∠BAD=30°,
∴∠OAF=∠CAD=![]() ∠BAD=15°,
∠BAD=15°,
∵∠OAE=∠AOE=45°,
∴∠EAF=30°,
∴AF=![]() =
=![]() ,EF=AEtan30°=
,EF=AEtan30°=![]() ,
,
∵AB=AD=4,AE∥DG,
∴![]() ,即
,即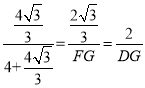
解得,FG=![]() ,DG=
,DG=![]()
∴EG=FG-FE=![]() -
-![]() =2,
=2,
∴OG=OE+EG=2+2=4,
∴D(4,![]() ),
),
∵D点D在函数y=![]() 的图象上,
的图象上,
∴k=4×(![]() )=8+8
)=8+8![]() .
.
故答案为:8+8![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目