题目内容
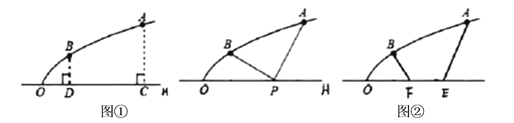
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B.

(1)如图,求证:BD+AB=![]() BC;
BC;
(2)直线MN绕点A旋转,在旋转过程中,当∠BCD=30°,BD=![]() 时,求BC的值.
时,求BC的值.
【答案】(1)证明见解析;(2)BC=![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】
(1)过点C作CE⊥CB于点C,与MN交于点E,易证:∠BCD=∠ACE,∠CBD=∠CEA,进而证明△ACE≌△DCB(AAS),可得:△ECB为等腰直角三角形,即:BE=![]() CB,进而得到结论;
CB,进而得到结论;
(2)分两种情况讨论:①当C,D在直线MN的同侧时,②当C,D在直线MN的异侧时,分别求出BC的值,即可.
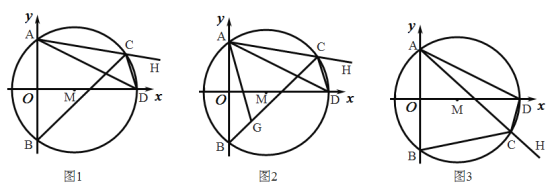
(1)过点C作CE⊥CB于点C,与MN交于点E,如图1,
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE,
∵DB⊥MN,
∴∠ABC+∠CBD=90°,
∵CE⊥CB
∴∠ABC+∠CEA=90°,
∴∠CBD=∠CEA.
又∵AC=DC,
∴△ACE≌△DCB(AAS),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() CB.
CB.
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=![]() CB.
CB.
(2)①当C,D在直线MN的同侧时,连接AD,过点D作DF⊥BC于点F,如图2,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠ADC=45°,
∵∠ACD=∠ABD=90°,
∴点A,点C,点D,点B四点共圆,
∴∠CAD=∠CBD=45°,且DF⊥BC,
∴∠FBD=∠FDB=45°,且BD=![]() ,
,
∴BF=DF=1,
∵∠BCD=30°,DF⊥BC,
∴CF=![]() DF=
DF=![]() ,
,
∴BC=CF+BF=![]() +1,
+1,
②当C,D在直线MN的异侧时,连接AD,过点D作DF⊥BC于点F,如图3,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠ADC=45°,
∵∠ACD=∠ABD=90°,
∴点A,点C,点D,点B四点共圆,
∴∠CAD=∠DBF=45°,且DF⊥BC,
∴∠FBD=∠FDB=45°,且BD=![]() ,
,
∴BF=DF=1,
∵∠BCD=30°,DF⊥BC,
∴CF=![]() DF=
DF=![]() ,
,
∴BC=CF﹣BF=![]() ﹣1.
﹣1.
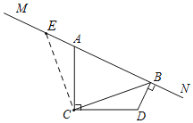
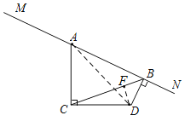
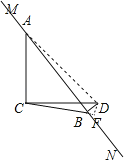
图1 图2 图3