Question

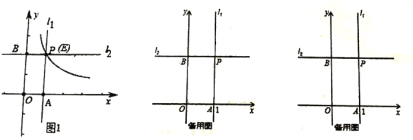
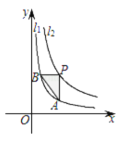
【题目】如图，函数(x>0)和(x>0)的图象分别是和.设点P在上，PA∥y轴交于点A，PB∥x轴，交于点B，△PAB的面积为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

将点P(m，n)代入反比例函数y=(x>0)用m表示出n即可表示出点P的坐标，然后根据PB∥x轴，得到B点的纵坐标为，然后将点B的纵坐标代入反比例函数的解析式y=(x>0)即可得到点B的坐标，同理得到点A的坐标；根据PB=m-=，PA=-=，利用S△PAB=PAPB即可得到答案.

解：设点P(m,n)，

∵P是反比例函数y=(x>0)图象上的点，

∴n=，

∴点P(m，)；

∵PB∥x轴，

∴B点的纵坐标为，

将点B的纵坐标代入反比例函数的解析式y=(x>0)得：x=，

∴B(，)，同理可得：A(m，)；

∵PB=m=，PA==，

∴S△PAB=PAPB=××=.

故选B.