题目内容
【题目】已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
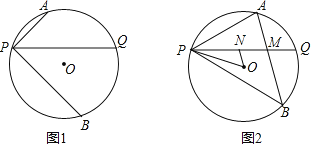
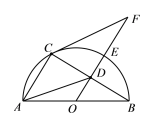
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径。
时,求⊙O的半径。
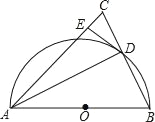
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
【答案】(1)![]() ;(2)α+2β=90°,见解析
;(2)α+2β=90°,见解析
【解析】
(1)连接AB,由已知得到∠APB=∠APQ+BPQ=90°,根据圆周角定理证得AB是⊙O的直径,然后根据勾股定理求得直径,即可求得半径;
(2)连接OA、OB、OQ,由![]() 证得∠APQ=∠BPQ,即可证得OQ⊥ON,然后根据三角形内角和定理证得2∠OPN+∠PON+∠NOQ=180°,,即可证得α+2β=90°.
证得∠APQ=∠BPQ,即可证得OQ⊥ON,然后根据三角形内角和定理证得2∠OPN+∠PON+∠NOQ=180°,,即可证得α+2β=90°.
(1)连接AB,
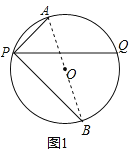
∵∠APQ=∠BPQ=45°,
∴∠APB=∠APQ+BPQ=90°,
∴AB是⊙O的直径,
∴AB=![]() ,
,
∴⊙O的半径为![]() ;
;
(2)α+2β=90°,
证明:连接OA、OB、OQ,

∵∠APQ=∠BPQ,
∴![]() ,
,
∴∠AOQ=∠BOQ,
∵OA=OB,
∴OQ⊥AB,
∵ON∥AB,
∴NO⊥OQ,
∴∠NOQ=90°,
∵OP=OQ,
∴∠OPN=∠OQP,
∵∠OPN+∠OQP+∠PON+∠NOQ=180°,
∴2∠OPN+∠PON+∠NOQ=180°,
∴∠NOP+2∠OPN=90°,
∵∠NOP=α,∠OPN=β,
∴α+2β=90°.
【解答】
解:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目