题目内容
【题目】已知:如图,△ABC内接于⊙O,点D在OC的延长线上,sinB= ![]() ,∠CAD=30°.
,∠CAD=30°.
(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=5,求AD的长.
【答案】
(1)
证明:连接OA,
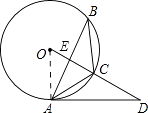
∵sinB= ![]() ,
,
∴∠B=30°,
∠AOC=60°,
又∵OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∴∠OAD=60°+30°=90°,
∴AD是⊙O的切线;
(2)
解:∵OC⊥AB,OC是半径,
∴BE=AE,
∴OD是AB的垂直平分线,
∴∠DAE=60°,∠D=30°,
在Rt△ACE中,AE=cos30°×AC= ![]() ,
,
∴在Rt△ADE中,AD=2AE=5 ![]() .
.
【解析】(1)连接OA,由于sinB= ![]() ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.