题目内容
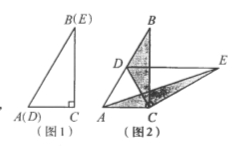
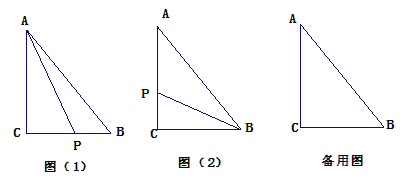
【题目】如图(1)在△ABC中,∠C=90°,AB=25cm,BC=15cm,若动点P从点C开始沿着C→B→A→C的路径运动,且速度为每秒5cm,设点P运动的时间为t秒.
(1)点P运动2秒后,求△ABP的面积;
(2)如图(2),当t为何值时,BP平分∠ABC;
(3)当△BCP为等腰三角形时,直接写出所有满足条件t的值.
【答案】(1)50(2)10.5(3)5.5、6、6.6、9
【解析】
(1)根据勾股定理求得AC=20,根据运动的速度和时间求得CP=10,BP=5,即可得到△ABP的面积;
(2)过点P作PD⊥AB于点D,判定Rt△BPD≌Rt△BPC(HL),得到BD=BC=15,AD=10,再设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,根据勾股定理得到PD2+AD2=AP2,即x2+102=(20﹣x)2,解方程即可得到结论;
(3)分三种情况讨论:①作CB的垂直平分线交AB于P,连接CP,则CP=BP;②以B为圆心,CB为半径作弧交AB于点P,则CB=PB=15;③以C为圆心,CB为半径作弧交AB于P1,交AC于点P2,过C作CD⊥AB于D,则CP1=CB,CP2=CB=15,分别求解即可.
(1)如图1.
∵∠C=90°,AB=25,BC=15,∴AC=![]() =20.
=20.
∵CP=5×2=10,BP=BC-PC=15-10=5,∴△ABP的面积=![]() ×PB×AC=
×PB×AC=![]() ×5×20=50(cm2).
×5×20=50(cm2).
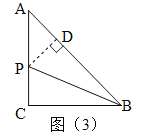
(2)如图(3),过点P作PD⊥AB于点D.
∵BP平分∠ABC,∴PD=PC.在Rt△BPD和Rt△BPC中,∵![]() ,∴Rt△BPD≌Rt△BPC(HL),∴BD=BC=15,∴AD=25﹣15=10,设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,PD2+AD2=AP2,即x2+102=(20﹣x)2,解得:x=7.5,∴t=(CB+BA+AC-PC)÷5=(15+25+20-7.5)÷5=10.5.
,∴Rt△BPD≌Rt△BPC(HL),∴BD=BC=15,∴AD=25﹣15=10,设PC=x,则PD=x,AP=20﹣x.在Rt△APD中,PD2+AD2=AP2,即x2+102=(20﹣x)2,解得:x=7.5,∴t=(CB+BA+AC-PC)÷5=(15+25+20-7.5)÷5=10.5.
故t=10.5秒时,BP平分∠ABC.
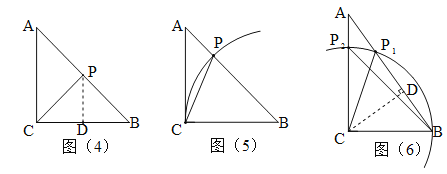
(3)分三种情况讨论:①如图(4),作CB的垂直平分线交AB于P,连接CP,则CP=BP.
∵AC⊥BC,PD⊥BC,∴AC∥PD.
∵CD=DB,∴AP=PB=![]() AB=12.5,∴t=(CB+BP)÷5=(15+12.5)÷5=5.5;
AB=12.5,∴t=(CB+BP)÷5=(15+12.5)÷5=5.5;
②如图(5),以B为圆心,CB为半径作弧交AB于点P,则CB=PB=15,∴t=(CB+BP)÷5=(15+15)÷5=6;
③如图(6),以C为圆心,CB为半径作弧交AB于P1,交AC于点P2,过C作CD⊥AB于D,则CP1=CB,CP2=CB,CD=![]() =
=![]() =12.
=12.
∵CP1=CB,CD⊥AB,∴BD=DP1=![]() =9,∴BP1=2BD=18,∴t=(15+18)÷5=6.6;
=9,∴BP1=2BD=18,∴t=(15+18)÷5=6.6;
∵CP2=CB=15,∴t=(CB+BA+AC-CP2)÷5=(15+25+20-15)÷5=9.
综上所述:当△BCP为等腰三角形时,t的值为:5.5,6,6.6,9.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案