��Ŀ����
����Ŀ����ͼ�������� ![]() ��ֱ��
��ֱ�� ![]() ����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����
����A��B���㣬��A��x���ϣ���B�ĺ�������2����P��ֱ��AB�Ϸ����������ϣ�����P�ֱ���PC��y�ᡢPD��x�ᣬ��ֱ��AB���ڵ�C��D����PC��PDΪ��������PCQD�����Q������Ϊ��m��n����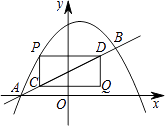
��1����A�������� �� ��B����������
��2������������������Ӧ�ĺ�����ϵʽ��
��3����m��n֮��ĺ�����ϵʽ����Ҫ��д���Ա���n��ȡֵ��Χ����
��4����ֱ��д������PCQD���ܳ����ʱn��ֵ��
���𰸡�
��1������2��0������2��2��
��2��
�⣺�����⣬�� 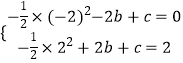 ��
��
��� ![]()
���ԣ���������������Ӧ�ĺ�����ϵʽΪy=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��3��
�⣺�ߵ�Q������Ϊ��m��n����
�� ![]() x+1=n��
x+1=n��
���x=2n��2��
���ԣ���C������Ϊ��2n��2��n����
��D��������m�� ![]() m+1����
m+1����
���P��������2n��2�� ![]() m+1����
m+1����
����2n��2�� ![]() m+1������y=��
m+1������y=�� ![]() x2+
x2+ ![]() x+3���é�
x+3���é� ![]() ����2n��2��2+
����2n��2��2+ ![]() ����2n��2��+3=
����2n��2��+3= ![]() m+1��
m+1��
�����ã�m=��4n2+10n��2��
���ԣ�m��n֮��ĺ�����ϵʽ��m=��4n2+10n��2��
��4��
�⣺��C��2n��2��n����P��2n��2�� ![]() m+1����Q��m��n����
m+1����Q��m��n����
��PC= ![]() m+1��n��CQ=m����2n��2��=m��2n+2��
m+1��n��CQ=m����2n��2��=m��2n+2��
�����PCQD���ܳ�=2�� ![]() m+1��n+m��2n+2����
m+1��n+m��2n+2����
=3m��6n+6��
=3����4n2+10n��2����6n+6��
=��12n2+24n��
=��12��n��1��2+12��
�൱n=1ʱ������PCQD���ܳ����
���������⣺��1����y=0���� ![]() x+1=0��
x+1=0��
���x=��2��
���ԣ���A����2��0����
�ߵ�B�ĺ�������2��
��y= ![]() ��2+1=2��
��2+1=2��
��B��2��2����
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

����Ŀ��2015��4��30�գ������⽭����ȫ��������ϣ����Ʒ��Ų���6460�ţ�ÿ���ϵIJ�����200�����ң����漰6�������漴��ʼ�������֣�С������¼�IJ��ַ�����������ʾ������Թ��Ʋ��ַ����ɹ��ĸ���Ϊ�� ��
�ۼƲ��ַ�������/�� | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
�����ɹ���/�� | 181 | 362 | 541 | 718 | 905 | 1077 | 1263 |
A.0.95
B.0.9
C.0.85
D.0.8




