��Ŀ����
����Ŀ����ͼ��ֱ��y1=�� ![]() x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����
x+2��x�ᣬy��ֱ���B��C��������y=ax2+bx+c��a��0��������A��B��C����A����Ϊ����1��0����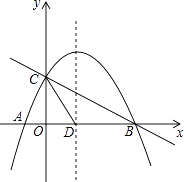
��1���������ߵĽ���ʽ��
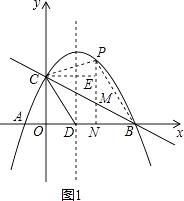
��2�������ߵĶԳ�����x�ύ�ڵ�D������CD����P��ֱ��BC�Ϸ��������ϵ�һ���㣨����B��C�غϣ�������P�˶����δ�ʱ���ı���PCDB�������������ʱ�ı���PCDB��������ֵ�͵�P���ꣻ
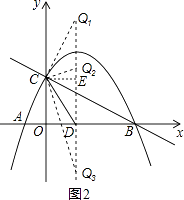
��3�����������ϵĶԳ������Ƿ����һ��Q��ʹ��QCD����CDΪ���ĵ��������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��x=0���ɵ�y=2��
��y=0���ɵ�x=4��
����B��4��0����C��0��2����
����κ����Ľ���ʽΪy=ax2+bx+c��
����A��B��C������������ʽ�ã�
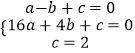 ��
��
��ã� 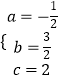 ��
��
���ö��κ����Ĺ�ϵʽΪy=�� ![]() x2+
x2+ ![]() x+2��
x+2��
��2��
�⣺��ͼ1������P��PN��x���ڵ�N����BC�ڵ�M������C��CE��PN��E��
��M��a���� ![]() a+2����P��a����
a+2����P��a���� ![]() a2+
a2+ ![]() a+2����
a+2����
��PM=�� ![]() a2+
a2+ ![]() a+2������
a+2������ ![]() a+2��=��
a+2��=�� ![]() a2+2a��0��x��4����
a2+2a��0��x��4����
��y=�� ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
���D���������� ![]() ��0����
��0����
��S�ı���PCDB=S��BCD+S��CPM+S��PMB= ![]() BDOC+
BDOC+ ![]() PMCE+
PMCE+ ![]() PMBN��
PMBN��
= ![]() +
+ ![]() a����
a���� ![]() a2+2a��+
a2+2a��+ ![]() ��4��a������
��4��a������
=��a2+4a+ ![]() ��0��x��4����
��0��x��4����
=����a��2��2+ ![]()
��a=2ʱ��S�ı���PCDB��������= ![]() ��
��
�ੁ ![]() a2+
a2+ ![]() a+2=��
a+2=�� ![]() ��22+
��22+ ![]() ��2+2=3��
��2+2=3��
���P��������2��3����
�൱��P�˶�����2��3��ʱ���ı���PCDB�����������ֵΪ ![]() ��
��
��3��
�⣺��ͼ2���������ߵĶԳ�����x= ![]() ��
��
��OD= ![]() ��
��
��C��0��2����
��OC=2��
��Rt��OCD�У��ɹ��ɶ�������
CD= ![]() ��
��
�ߡ�CDQ����CDΪ���ĵ��������Σ�
��CQ1=DQ2=DQ3=CD��
��ͼ2��ʾ����CE�ͶԳ�����E��
��EQ1=ED=2��
��DQ1=4��
��Q1�� ![]() ��4����Q2��
��4����Q2�� ![]() ��
�� ![]() ����Q3��
����Q3�� ![]() ����
���� ![]() ����
����
����������1���ֱ������ʽy=�� ![]() x+2��x=0��y=0�������B����C�����ꣻ����κ����Ľ���ʽΪy=ax2+bx+c������A��B��C������������ʽ�����a��b��c��ֵ��������ý���ʽ����2�����M�������Ϊ��a����
x+2��x=0��y=0�������B����C�����ꣻ����κ����Ľ���ʽΪy=ax2+bx+c������A��B��C������������ʽ�����a��b��c��ֵ��������ý���ʽ����2�����M�������Ϊ��a���� ![]() a+2�����Ϳ��Ա�ʾ��P�����꣬���ı���PCDB�����=S��BCD+S��CPM+S��PMB���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ���3���ɣ�2���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����Q1 �� �Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�Q2 �� Q3 �� ��CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
a+2�����Ϳ��Ա�ʾ��P�����꣬���ı���PCDB�����=S��BCD+S��CPM+S��PMB���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ���3���ɣ�2���Ľ���ʽ����������꣬���ɹ��ɶ������CD��ֵ�����Ե�CΪԲ�ģ�CDΪ�뾶�������Գ�����Q1 �� �Ե�DΪԲ��CDΪ�뾶��Բ���Գ����ڵ�Q2 �� Q3 �� ��CE��ֱ�ڶԳ������E���ɵ��������ε����ʼ����ɶ����Ϳ���������ۣ�
�����㾫�������ö��κ�����ͼ�����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮