Question

【题目】济宁市“五城同创”活动中，一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成.

（1）求乙工程队单独完成这项工作需要多少天？

（2）因工期的需要，将此项工程分成两部分，甲做其中一部分用了x天完成，乙做另一部分用了y天完成，其中x、y均为正整数，且x<46，y<52，求甲、乙两队各做了多少天？

Answer 1

【答案】（1）乙工程队单独做需要80天完成；（2）甲队做了45天，乙队做了50天.

【解析】

（1）根据“甲工程队单独完成这项工作需120天，甲工程队单独工作30天后，乙工程队参与合做，两队又共同工作了36天完成”，设乙工程队单独完成这项工作需要x天，列出方程求解即可；

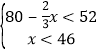（2）因为甲队做其中一部分用了x天，乙队做另一部分用了y天，可得到方程，再根据x<46，y<52，得到方程组，其中x、y均为正整数，解此方程组即可得到答案.

（1）设乙工程队单独完成这项工作需要x天，由题意得

，解之得x=80.·

经检验x=80是原方程的解.

答：乙工程队单独做需要80天完成.

（2）因为甲队做其中一部分用了x天，乙队做另一部分用了y天，

所以，即，又x<46，y<52，

所以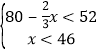，解之得42<x<46，

因为x、y均为正整数，所以x=45，y=50.

答：甲队做了45天，乙队做了50天.·