题目内容
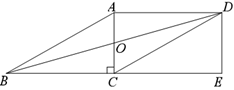
【题目】在平面直角坐标系![]() 中,如果等边三角形的一边与
中,如果等边三角形的一边与![]() 轴平行或在
轴平行或在![]() 轴上,则称这个等边三角形为水平正三角形.
轴上,则称这个等边三角形为水平正三角形.
(1)已知![]() ,
,![]() ,若
,若![]() 是水平正三角形,则点
是水平正三角形,则点![]() 坐标的是_____(只填序号);①
坐标的是_____(只填序号);①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
(2)已知点![]() ,
,![]() ,
,![]() ,以这三个点中的两个点及平面内的另一个点
,以这三个点中的两个点及平面内的另一个点![]() 为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点
为顶点,构成一个水平正三角形,则这两个点是 ,并求出此时点![]() 的坐标;
的坐标;
(3)已知![]() 的半径为
的半径为![]() ,点
,点![]() 是
是![]() 上一点,点
上一点,点![]() 是直线
是直线![]() 上一点,若某个水平正三角形的两个顶点为
上一点,若某个水平正三角形的两个顶点为![]() ,
,![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)点![]() 坐标的是②,④;(2)
坐标的是②,④;(2)![]() 或
或![]() ;(3)点
;(3)点![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]()
![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用勾股定理求出![]() 的长,即可知道
的长,即可知道![]() 的坐标;
的坐标;
(2)因为是一个水平正三角形,则这两个点是![]() ,
,![]() ,连接
,连接![]() ,所以
,所以![]() 与
与![]() 轴正方向夹角为
轴正方向夹角为![]() ,然后分①当点
,然后分①当点![]() 在线段
在线段![]() 的左侧时和②当点
的左侧时和②当点![]() 在线段
在线段![]() 的右侧时两种情况讨论;
的右侧时两种情况讨论;
(3)分三种情况:①当![]() 与
与![]() 轴平行或重合时;②当
轴平行或重合时;②当![]() 与
与![]() 轴的负半轴夹角为
轴的负半轴夹角为![]() 时;③当
时;③当![]() 与
与![]() 轴的正半轴夹角为
轴的正半轴夹角为![]() 时;根据水平正三角形的性质求出点
时;根据水平正三角形的性质求出点![]() 的横坐标
的横坐标![]() 的取值范围即可.
的取值范围即可.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
当点![]() 在
在![]() 轴上方时,
轴上方时,![]() ,
,
当点![]() 在
在![]() 轴下方时,
轴下方时,![]() ,
,
则点![]() 坐标的是②,④;
坐标的是②,④;
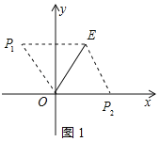
(2)因为是一个水平正三角形,则这两个点是![]() ,
,![]() ,连接
,连接![]() ,如图1所示:
,如图1所示:
∴![]() 与
与![]() 轴正方向夹角为
轴正方向夹角为![]() .
.
①当点![]() 在线段
在线段![]() 的左侧时,
的左侧时,
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,
,
②当点![]() 在线段
在线段![]() 的右侧时,
的右侧时,
点![]() 在
在![]() 轴上且
轴上且![]() ,
,
∴![]() .
.
∴![]() 或
或![]() ;
;
(3)分三种情况:
①当![]() 与
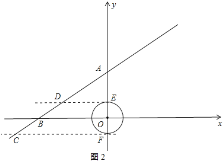
与![]() 轴平行或重合时,如图2所示:
轴平行或重合时,如图2所示:
![]() 为
为![]() 的直径,直线
的直径,直线![]() 与坐标轴的交点分别为
与坐标轴的交点分别为![]() 、
、![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
作![]() 轴交直线
轴交直线![]() 于
于![]() ,作
,作![]() 轴交直线
轴交直线![]() 于
于![]() ,
,
则![]() 在线段
在线段![]() 上,
上,![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴![]() ;
;
②当![]() 与
与![]() 轴的负半轴夹角为
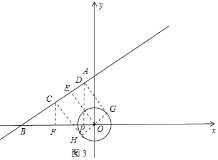
轴的负半轴夹角为![]() 时,如图3所示:
时,如图3所示:
作![]() 直线
直线![]() 于
于![]() ,作直径
,作直径![]() ,作
,作![]() 、
、![]() ,分别交
,分别交![]() 于
于![]() 、
、![]() ,
,
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,
,
则![]() 在线段
在线段![]() 上,
上,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
同理:![]() ,
,
∴![]() ;
;
③当![]() 与
与![]() 轴的正半轴夹角为
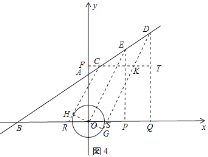
轴的正半轴夹角为![]() 时,如图4所示:
时,如图4所示:
同②得:![]() .
.
综上所述,点![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目