题目内容
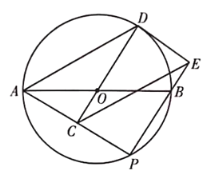
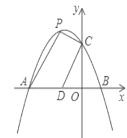
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ,
,![]() ;②
;②![]() ,
,![]() (-1,5).
(-1,5).
【解析】
(1)设抛物线的表达式为:y=a(x+3)(x1)=a(x2+2x3)=ax2+2ax3a,即3a=2,解得:a=![]() ,即可求解;
,即可求解;
(2)设点P(x,![]() ),根据S=S四边形ADCP=S△APO+S△CPOS△ODC=4列出方程即可求解;
),根据S=S四边形ADCP=S△APO+S△CPOS△ODC=4列出方程即可求解;
(3)①根据等腰直角三角形的性质,构造全等三角形即可求出M的坐标;
②根据题意作图,根据①所求的M点坐标结合圆周角的性质与等腰直角三角形的性质即可确定N点坐标.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]()
设抛物线的表达式为:y=a(x+3)(x1)=a(x2+2x3)=ax2+2ax3a,
∴3a=2,解得:a=![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)令x=0,得y=2
∴点C(0,2),
函数的对称轴为:x=-  =-1;
=-1;
连接OP,设点P(x,![]() ),
),
则S=S四边形ADCP=S△APO+S△CPOS△ODC
=![]() ×AO×yp+
×AO×yp+![]() ×OC×|xP|
×OC×|xP|![]() ×CO×OD
×CO×OD
=![]() ×3×(
×3×(![]() )+
)+![]() ×2×(x)
×2×(x) ![]() ×2×1
×2×1
=x23x+2,
∵四边形![]() 面积等于4,
面积等于4,
∴x23x+2=4
解得x1=-1,x2=-2,
∴P![]() 或
或![]() ;
;
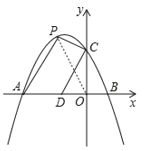
(3) ①如图,∵△CDM1是以CM1为斜边的等腰直角三角形,
∴CD=DM1,∠CDM=90°,
∴∠QDM1+∠CDO=90°
作M1Q⊥AB于Q点,
∴∠QDM1+∠QM1D=90°
∴∠CDO=∠QM1D
又∠DQM1=∠COD=90°
∴△DQM1≌△COD
QD=CO=2,M1Q=DO=1
∴OD=3, M1Q=1
∴M1(-3,1)
由图形及等腰直角三角形的性质可知M1、M2关于D点对称,
设M2(p,q)
∴![]() ,
,![]()
解得p=1,q=-1
∴M2(1,-1)
综上M的坐标为![]() ,
,![]() ;
;
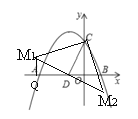
②如图,∵![]() =90°,当
=90°,当![]() =
=![]()
![]() 可知N点为对称轴直线x=-1与以圆D为圆心,DM2为半径的圆的交点,即N1,N2
可知N点为对称轴直线x=-1与以圆D为圆心,DM2为半径的圆的交点,即N1,N2
∵r=DM2=![]()
∴N1(-1,-![]() ),N2(1,
),N2(1,![]() );
);

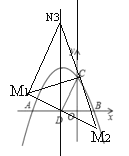
如图,当![]() 时,
时,
由①可得![]() ,
,![]() ,
,
∴![]() ,CD=DM1=DM2,
,CD=DM1=DM2,
∴CM1=CM2,
则△![]() 是等腰直角三角形,
是等腰直角三角形,
则![]()
∴△![]() 是等腰直角三角形,
是等腰直角三角形,
则N3,M2关于C点对称,
设N3(x,y)
则![]() ,
,![]()
解得x=-1,y=5
∴N3(-1,5)
综上,N点坐标为:![]() ,
,![]() (-1,5).
(-1,5).

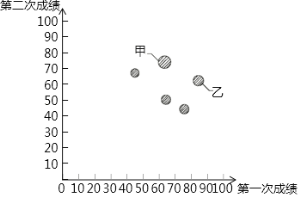
【题目】甲、乙两人进行射击比赛,两人4次射击的成绩(单位:环)如下:
甲:8,6,9,9;
乙:7,8,9,8.
(1)请将下表补充完整:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 1.5 | ||
乙 | 8 | 8 |
(2)谁的成绩较稳定?为什么?
(3)分别从甲、乙两人的成绩中随机各选取一次,则选取的两个成绩之和为16环的概率是多少?
【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.