题目内容
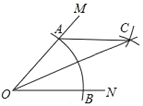
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
【答案】![]() .
.
【解析】
根据题意,作出合适的辅助线,然后根据角平分线的性质、等腰三角形的性质和勾股定理可以求得点B到AC的距离,本题得以解决.
由题意可得,OC为∠MON的角平分线,
∵OA=OB,OC平分∠AOB,
∴OC⊥AB,
设OC与AB交于点D,作BE⊥AC于点E,连接BC,
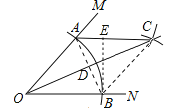
∵AB=6,OA=5,AC=OA,OC⊥AB,
∴AC=5,∠ADC=90°,AD=3,
∴CD=4,
由三角形面积计算可得,![]() .
.
∴![]() ,
,
解得,BE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】“十一”黄金周期间,某动物园在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数,并直接写出七天内游客人数最多的是哪一天?
日的游客人数,并直接写出七天内游客人数最多的是哪一天?
(2)若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,门票每人
万人,门票每人![]() 元,问黄金周期间该动物园门票总收入是多少万元?
元,问黄金周期间该动物园门票总收入是多少万元?