Question

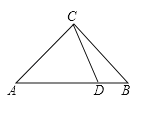
【题目】已知：在Rt△ABC中，∠ACB=90°，AC=BC，D是线段AB上一点，连结CD，将线段CD绕点C逆时针旋转90°得到线段CE，连结DE，BE．

（1）依题意补全图形；

（2）若∠ACD=α，用含α的代数式表示∠DEB；

（3）若△ACD的外心在三角形的内部，请直接写出α的取值范围．

Answer 1

【答案】（1）作图见解析；（2）90°﹣α；（3）45°＜α＜90°．

【解析】

（1）依据几何语言进行作图即可；

（2）依据△ACD≌△BCE，即可得到∠CBE＝∠A，再根据三角形内角和定理，即可用含α的代数式表示∠DEB；

（3）根据锐角三角形的外心位于三角形内部，即可得出α的取值范围．

解：（1）如图，CE、BE、DE为所作；

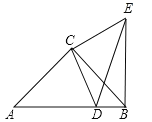
（2）∵将线段CD绕点C 逆时针旋转90°得到线段CE，

∴∠DCE＝90°，CD＝CE

∵∠ACB＝90°，

∴∠ACD＝∠BCE＝α，

在△ACD和△BCE中，

，

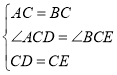∴△ACD≌△BCE (SAS)，

∴∠CBE＝∠A．

∵∠ACB＝90°，AC＝BC

∴∠A＝45°

∴∠CBE＝45°

∵∠DCE＝90°，CD＝CE

∴∠CED＝45°，

在△BCE中，∠BCE＝∠ACD＝α．

∴∠DEB＝180°﹣α﹣45°﹣45°＝90°﹣α．

（3）∵△ACD的外心在三角形的内部，

∴△ACD是锐角三角形，

∴∠ACD＜90°，∠ADC＜90°，

又∵∠A＝45°，

∴∠ACD＞45°，

∴45°＜α＜90°．