��Ŀ����
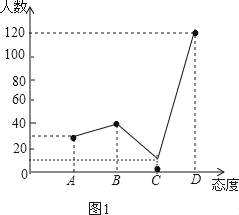
����Ŀ��Ŀǰ��У�ֻ�������Խ��Խ�ܵ�����ע�������������ijУ���꼶��ѧ��ȤС���ͬѧ����������������ҳ�������ѧ�����ֻ�������̬�ȣ�̬�ȷ�Ϊ��A������ν��B�������ɣ�C���ɣ�D�����ԣ����������������Ƴ�Ƶ������ͳ��ͼ1������ͳ��ͼ2�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������˶�������ѧ���ҳ���
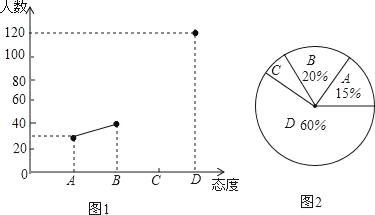
��2�����ͼ2������C���Ե�Բ�ĽǵĶ���������ͼ1����������
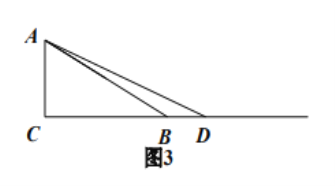
��3���ڴ˴ε����У�������1������A1��A2��λ�ҳ�����ѧ�����ֻ��ַ���̬�ȣ�������2������B1��B2��λѧ���ҳ�����ѧ�����ֻ�Ҳ�ַ���̬�ȣ��ִ���4λ�ҳ���ѡ2λ�ҳ��μ�ѧУ��֯�ļ�У������б�������״ͼ�ķ������ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
���𰸡���1��200����2�������������3��![]()
��������
��1����D���������������ռ�İٷֱȼ��ɵõ��������������
��2����360������C����ռ�İٷֱȵõ�����C���Ե�Բ�ĽǵĶ���������200����C����ռ�İٷֱȵõ�C��������Ȼ��ȫͼ1��
��3������״ͼչʾ����12�ֵȿ��ܽ�������ҳ�2�����Բ�ͬ�༶�Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�⣺��1��120��60%��200���ˣ���
���Ե���ļҳ���Ϊ200�ˣ�
��2������C���Ե�Բ�ĽǵĶ�����360�����1��20%��15%��60%����18����
C��ļҳ�����200����1��20%��15%��60%����10���ˣ���
����ͼΪ��
��3���������1���������ҳ�ΪA1��A2��������2���������ҳ�ΪB1��B2��
����״ͼΪ
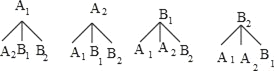
����12�ֵȿ��ܽ��������2�����Բ�ͬ�༶����8�֣�
����2�����Բ�ͬ�༶�ĸ��ʣ�![]() ��
��![]() ��
��

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�����Ŀ��ij�������ƻ�Ϊũ������ũ���豸�ṩ���������й������͡������豸ũ����Ͷ�ʵĽ�������������Ķ�ȴ����±���ʾ�ĺ�����Ӧ��ϵ��
�ͺ� ��� | �����豸 | �����豸 | |||
Ͷ�ʽ��x����Ԫ�� | x | 5 | x | 2 | 4 |
�������y����Ԫ�� | y1��kx��k��0�� | 2 | y2��ax2+bx��a��0�� | 2.8 | 4 |
��1���ֱ���y1��y2�ĺ�������ʽ��
��2����һũ����Ͷ��10��Ԫ�������͡����������豸�������豸��Ͷ�ʾ�Ϊ������Ԫ��Ҫ�����������Ӧ����ι����ܻ�õ���������Ϊ���٣�
����Ŀ��ijˮ�������г��涨������ƻ��������![]() ʱ��������Ϊ5Ԫ/
ʱ��������Ϊ5Ԫ/![]() ��С��Я���ֽ�4000Ԫ�����г��ɹ�ƻ�������������������
��С��Я���ֽ�4000Ԫ�����г��ɹ�ƻ�������������������
���������⣬�����
�������� |
|
|
|
|
���� |
|
| ||
ʣ���ֽ� |
|
|
�����蹺���ƻ��Ϊ![]() ��С�������ʣ���ֽ�
��С�������ʣ���ֽ�![]() Ԫ����
Ԫ����![]() ����
����![]() �ĺ�������ʽ����ָ���Ա���
�ĺ�������ʽ����ָ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������������գ���С��ʣ���ֽ�Ϊ700Ԫ����������__________![]() ��ƻ����
��ƻ����