题目内容
【题目】已知，如图A、B分别为数轴上的两点，A点对应的数为-10 ，B点对应的数为90.
（1）请写出AB的中点M对应的数.
（2）现在有一只电子蚂蚁P从B点出发，以3个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以2个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C点相遇，
①你知道经过几秒两只电子蚂蚁相遇？
②点C对应的数是多少？
③经过多长时间两只电子蚂蚁在数轴上相距10个单位长度？
【答案】（1）40；（2）①20秒；②30；③18秒.
【解析】
⑴求-10和90的中点，直接利用数轴上两点间中点求法得出答案；⑵①设所用时间为t,列出一元一次方程求出即可；②利用B点数值减去P所走的距离即可；③设时间为x列出一元一次方程即可求出.
解：⑴
=40
⑵ ①设所用时间为t，依题意得：3t﹢2t=100 解得t=20
②依题意得：点C位置为 90-3t=90-3×20=30
③设所用时间为x，依题意得：3x+2x=90 解得x=18
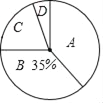
【题目】2017年4月15日至5月15日，某市约8万名初三毕业生参加了中考体育测试，为了了解今年初三毕业生的体育成绩，从某校随机抽取了60名学生的测试成绩，根据测试评分标准，将他们的得分按优秀、良好、及格、不及格（分别用A、B、C、D表示）四个等级进行统计，并绘制成下面的扇形图和统计表：
等级 | 成绩（分） | 频数（人数） | 频率 |
A | 27～30 | 24 | 0.4 |
B | 23～26 | m | x |
C | 19～22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合计 | 60 | 1.00 |
请你根据以上图表提供的信息，解答下列问题：
（1）m= ，n= ，x= ，y= ；
（2）在扇形图中，B等级所对应的圆心角是 度；
（3）请你估计某市这8万名初三毕业生成绩等级达到优秀和良好的大约有多少人？
（4）初三（1）班的甲、乙、丙、丁四人的成绩均为A，现决定从这四名同学中选两名参加学校组织的体育活动，直接写出恰好选中甲、乙两位同学的概率．
