题目内容
【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
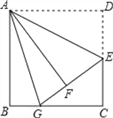
A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;
在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,
在Rt△ABG和Rt△AFG中,AG=AG,AB=AF, ∴Rt△ABG≌Rt△AFG(HL),
∴BG=GF,∵E是边CD的中点,∴DE=CE=6,
设BG=x,则CG=12-x,GE=x+6,∵GE2=CG2+CE2, ∴(x+6)2=(12-x)2+62,
解得:x=4, ∴BG=4. 故选B.

【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.