题目内容
【题目】阅读下列材料，并解答其后的问题：
我国古代南宋数学家秦九韶在其所著书《数学九章》中，利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题，这与西方著名的“海伦公式”是完全等价的．我们也称这个公式为“海伦秦九韶公式”，该公式是：设△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，△ABC的面积为S＝
．
（1）（举例应用）已知△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，且a＝4，b＝5，c＝7，则△ABC的面积为 ；
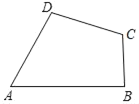
（2）（实际应用）有一块四边形的草地如图所示，现测得AB＝（2
+4
）m，BC＝5m，CD＝7m，AD＝4m，∠A＝60°，求该块草地的面积．
【答案】（1）
（2）（12
+24+5
）m2
【解析】
（1）由已知△ABC的三边a=4，b=5，c=7，可知这是一个一般的三角形，故选用海伦-奏九韶公式求解即可；（2）过点D作DE⊥AB，垂足为E，连接BD.将所求四边形的面积转化为三个三角形的面积的和进行计算。
（1）解：△ABC的面积为S＝
＝
＝4
故答案是：4；
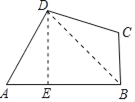
（2）解：如图：过点D作DE⊥AB，垂足为E，连接BD（如图所示）
在Rt△ADE中，
∵∠A＝60°，
∴∠ADE＝30°，
∴AE＝
AD＝2
∴BE＝AB﹣AE＝2+4
﹣2＝4
DE＝
∴BD＝
∴S△BCD＝
∵S△ABD＝
∴S四边形ABCD＝S△BCD+S△ABD＝ 
答：该块草地的面积为（）m2．
【题目】为了更好的治理西流湖水质，保护环境，市治污公司决定购买 10 台污水处理设备．现有 A、B 两种型号的设备，其中每台的价格，月处理污水量如下表：
A 型 | B 型 | |
价格（万元/台） | a | b |
处理污水量（吨／月） | 240 | 200 |
经调查：购买一台 A 型设备比购买一台 B 型设备多 2 万元，购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元．
（1）求 a，b 的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过 105 万元，你认为该公司 有哪几种购买方案；
（3）在（2）问的条件下，若每月要求处理西流湖的污水量不低于 2040 吨，为了节 约资金，请你为治污公司设计一种最省钱的购买方案．
【题目】6月14日是“世界献血日”，某市采取自愿报名的方式组织市民义务献血．献血时要对献血者的血型进行检测，检测结果有“A型”、“B型”、“AB型”、“O型”4种类型．在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表：
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
（1）这次随机抽取的献血者人数为 人，m= ；
（2）补全上表中的数据；
（3）若这次活动中该市有3000人义务献血，请你根据抽样结果回答：
从献血者人群中任抽取一人，其血型是A型的概率是多少？并估计这3000人中大约有多少人是A型血？
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题：
（1）完成下表：
姓名 | 平均成绩（分） | 中位数（分） | 众数（分） | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
（2）在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？
（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．
