题目内容
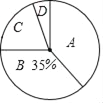
【题目】2017年4月15日至5月15日,某市约8万名初三毕业生参加了中考体育测试,为了了解今年初三毕业生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 27~30 | 24 | 0.4 |
B | 23~26 | m | x |
C | 19~22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合计 | 60 | 1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= ,n= ,x= ,y= ;
(2)在扇形图中,B等级所对应的圆心角是 度;
(3)请你估计某市这8万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
【答案】(1)21,12,0.35,0.2;(2)126.(3)6万人;(4)![]()
【解析】分析:(1)让总人数60乘以相应的百分比35%可得m的值,让总人数60减去其余已知人数可得n的值,x为相应百分比,将n的值除以60即为y的值;
(2)让360乘以相应频率即为B等级所对应的圆心角;
(3)该市初三毕业生总人数8万人乘以A、B两个等级的百分比的和即为所求的人数;
(4)列出从甲、乙、丙、丁四人选两人的6种结果,选中甲、乙两位同学的结果只有1种,由概率公式可得.
详解:(1)m=60×35%=21,n=60﹣21﹣24﹣3=12,x=35%=0.35,y=12÷60=0.2;
(2)B等级所对应的圆心角35%×360°=126°;
(3)由上表可知达到优秀和良好的共有21+24=45人,8×![]() =6(万人),
=6(万人),
答:估计这8万名初三毕业生成绩等级达到优秀和良好的大约有6万人;
(4)∵从甲、乙、丙、丁四人选两人有如下6种结果:
(甲,乙)、(甲,丙)、(甲,丁)、(乙,丙)、(乙,丁)、(丙,丁),
恰好选中甲、乙两位同学的结果只有1种,
∴恰好选中甲、乙两位同学的概率为![]() ;
;
故答案为:(1)21,12,0.35,0.2;(2)126.

【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.