题目内容
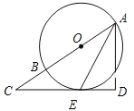
【题目】如图,AB是⊙O的直径,过点E作⊙O的切线ED,AD⊥ED于D,直线ED交AB的延长线于点C.
(1)求证:AE平分∠CAD.
(2)若BC=2,CE=4,求⊙O的半径.
【答案】(1)证明见详解,(2)3.
【解析】
(1)连接OE,首先利用切线性质得到OE⊥GE,而AD⊥CE,由此得到OE∥AD,然后利用平行线的性质和等腰三角形的性质即可求解;
(2)设⊙O的半径为r,在Rt△CEO中利用勾股定理可以列出关于r的方程,解方程求出r.
解:(1)如图示,连接OE,
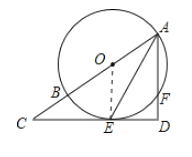
∵CE是⊙O的切线,
∴OE⊥CE,
∵AD⊥CE,
∴OE∥AD,
∴∠OEA=∠DAE,
∵OE=OA,
∴∠CAE=∠OEA,
∴∠CAE =∠DAE,
∴AE是∠CAD的角平分线;
(2)设⊙O的半径为r,
在Rt△CEO中,∵![]() ,CB=2,CE=4,
,CB=2,CE=4,
∴![]() ,
,
∴![]() ,
,

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目