题目内容
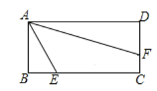
【题目】如图,E、F分别是正方形ABCD的边BC、CD的中点,连接AF、DE交于点P,过B作BG∥DE交AD于G,BG与AF交于点M.对于下列结论:①AF⊥DE;②G是AD的中点;③∠GBP=∠BPE;④S△AGM:S△DEC=1:4.正确的个数是( )
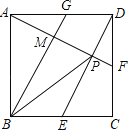
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形性质得出![]() ;
;![]() ;
;![]() ,证
,证![]() ≌
≌![]() ,推出
,推出![]() ,求出
,求出![]() 即可判断
即可判断![]() ;证明四边形GBED为平行四边形,则可知
;证明四边形GBED为平行四边形,则可知![]() 正确;由平行线的性质可得
正确;由平行线的性质可得![]() 正确;证明
正确;证明![]() ∽
∽![]() ,可得出
,可得出![]() :
:![]() :
:![]() 则
则![]() 不正确.
不正确.
解:∵正方形ABCD,E,F均为中点
∴AD=BC=DC,EC=DF=![]() BC,
BC,
∵在△ADF和△DCE中,
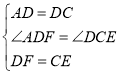 ,
,
∴△ADF≌△DCE(SAS),
∴∠AFD=∠DEC,
∵∠DEC+∠CDE=90°,
∴∠AFD+∠CDE=90°=∠DGF,
∴AF⊥DE,故①正确,
∵![]() ,
,![]() ,
,
∴四边形GBED为平行四边形,
∴GD=BE,
∵BE=![]() BC,
BC,
∴GD=![]() AD,
AD,
即G是AD的中点,
故②正确,
∵![]() ,
,
∴∠GBP=∠BPE,
故③正确.
∵![]() ,AF⊥DE,
,AF⊥DE,
∴AF⊥BG,
∴∠ANG=∠ADF=90°,
∵∠GAM=∠FAD,
∴△AGM∽△AFD,
设AG=a,则AD=2a,AF=![]() a,
a,
∴![]() .
.
∵△ADF≌△DCE,
∴S△AGM:S△DEC=1:5.
故④错误.
故选:C.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目