Question

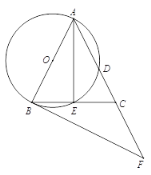
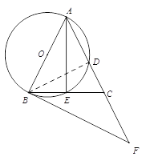
【题目】如图，在△ABC 中，AB = AC，以AB为直径的⊙O 分 别交AC，BC于点 D，E，过点B作⊙O的切线， 交 AC的延长线于点F．

(1) 求证：∠CBF =∠CAB；

(2) 若CD = 2，，求FC的长．

Answer 1

【答案】（1）见解析；（2）FC= .

【解析】

（1）利用等腰三角形的性质易证∠BAE=∠EAC=∠CAB，由弦切角定理可得∠BAE=∠CBF，即可证明.
（2）连接BD，由∠DBC=∠CBF. 得到tan∠DBC=.得出BD=4. 设AB=x，则AD= ，在RtΔABD中，根据勾股定理求得AB=5，证明ΔABD∽ΔAFB，根据相似三角形的性质即可求解.

（1）证明：∵AB 为⊙O的直径，

∴∠AEB=90°.

∴∠BAE+∠ABC=90°，

∵AB = AC，

∴∠BAE=∠EAC=∠CAB.

∵BF为⊙O 的切线，

∴∠ABC+∠CBF=90°.

∴∠BAE=∠CBF.

∴∠CBF =∠CAB.

（2）解：连接BD，

∵AB 为⊙O的直径，

∴∠ADB=90°.

∵∠DBC=∠DAE，

∴∠DBC=∠CBF.

∵tan∠CBF=.

∴tan∠DBC=.

∵CD=2，

∴BD=4.

设AB=x，则AD= ，

在RtΔABD中，∠ADB=90°，由勾股定理得x=5.

∴AB=5，AD=3.

∵∠ABF=∠ADB=90°，∠BAF=∠BAF.

∴ΔABD∽ΔAFB.

∴.

∴AF=.

∴FC=AF-AC=.