Question

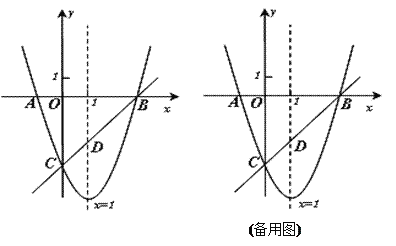
【题目】在平面直角坐标系中，点，点.已知抛物线（是常数），顶点为.

（Ⅰ）当抛物线经过点时，求顶点的坐标；

（Ⅱ）若点在轴下方，当时，求抛物线的解析式；

（Ⅲ） 无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.

Answer 1

【答案】（Ⅰ）；（Ⅱ）；（Ⅲ）或.

【解析】（Ⅰ）把点A（1，0）代入求出m的值，从而确定二次函数解析式，进而求出顶点P的坐标；

（Ⅱ）先由函数解析式得出顶点坐标为.再结合已知条件可知，从而求出，.再进行分类讨论得到抛物线解析式为；

（Ⅲ）由 可知，定点H的坐标为，过点作，交射线于点，分别过点，作轴的垂线，垂足分别为，，则可证.得点的坐标为或.然后进行分类讨论即可求解.

（Ⅰ）∵抛物线经过点，

∴，解得.

∴抛物线的解析式为.

∵ ，

∴顶点的坐标为.

（Ⅱ）抛物线的顶点的坐标为.

由点在轴正半轴上，点在轴下方，，知点在第四象限.

过点作轴于点，则.

可知，即，解得，.

当时，点不在第四象限，舍去.

∴.

∴抛物线解析式为.

（Ⅲ）由 可知，

当时，无论取何值，都等于4.

得点的坐标为.

过点作，交射线于点，分别过点，作轴的垂线，垂足分别为，，则.

∵，，

∴.∴.

∵ ，

∴.

∴.

∴，.

可得点的坐标为或.

当点的坐标为时，可得直线的解析式为.

∵点在直线上，

∴.解得，.

当时，点与点重合，不符合题意，∴.

当点的坐标为时，

可得直线的解析式为.

∵点在直线上，

∴ .解得（舍），.

∴.

综上，或.

故抛物线解析式为或.