Question

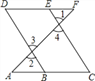
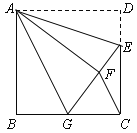
【题目】如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．

（1）求证：①△ABG≌△AFG； ②BG＝GC；

（2）求△FGC的面积.

Answer 1

【答案】（1）①见解析，②见解析；（2）

【解析】

（1）①根据折叠的性质可得∠B＝∠AFG＝90，AB＝AF，AG＝AG，根据HL定理即可证两三角形全等；②设BG＝FG＝x，（x＞0），则CG＝6－x，EG＝2＋x，在Rt△CEG中，利用勾股定理即可列方程求解；（2）根据三角形的面积公式可得：S△FGC=S△EGC，即可求解.

（1）证明：

①在正方形ABCD中，AD＝AB，∠D＝∠B＝∠C＝90

又∵△ADE沿AE对折至△AFE，延长EF交边BC于点G

∴∠AFG＝∠AFE＝∠D＝90，AF＝AD，

即有∠B＝∠AFG＝90，AB＝AF，AG＝AG，

∴△ABG≌△AFG

②∵AB＝6，点E在边CD上，且CD＝3DE，∴DE＝FE＝2，CE＝4

不妨设BG＝FG＝x，（x＞0），则CG＝6－x，EG＝2＋x，

在Rt△CEG中，(2＋x)2＝42＋(6－x)2

解得x＝3，于是BG＝GC＝3

（2）∵,∴

∴S△FGC=S△EGC=