Question

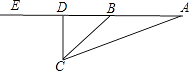
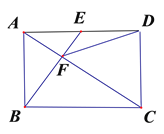
【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，

（1）求证：CF＝2AF；

（2）求tan∠CFD的值．

Answer 1

【答案】（1）证明见解析；（2）tan∠CFD=

【解析】试题分析：(1)已知矩形ABCD中，根据矩形的性质可得AD∥BC，即可判定△AEF∽△CAB，根据相似三角形的性质可得AF：CF=AE：BC=1：2，即可得CF＝2AF；（2）过D作DH⊥AC于H，可得DH∥BE，即可得AF：FH=AE：ED=1：1所以AF=FH=HC设AF=，则AH=2 CH=，易证Rt△ADH∽Rt△DCH，求得 BF=，所以tan∠CFD=.

试题解析：

(1) ∵ABCD为矩形， ∴AD∥BC，AD=BC， ∠D=90°,

∴△AEF∽△CBF，

∵E是AD边的中点， ∴AF：CF=AE：BC=1：2

∴CF＝2AF；

(2) 过D作DH⊥AC于H，

∵BE⊥AC，∴DH∥BE

∴AF：FH=AE：ED=1：1

∴AF=FH=HC

设AF=，则AH=2 CH=

∵∠DAH=∠CDH=90°-∠ADH

易知：Rt△ADH∽Rt△DCH，∴ BF=

∴tan∠CFD=