题目内容
【题目】如图,在四边形ABCD中,AD∥BC,F在CD上,且AF垂直平分CD,FG平分∠AFD,交AD于G,连接GB,交AF于N,且FN=FD.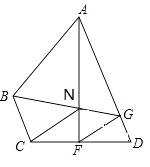
(1)求证:△GFN≌△GFD;
(2)如图,连接ND,若BC=ND,∠ADC=75°,求证:AN=AB;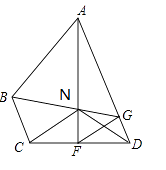
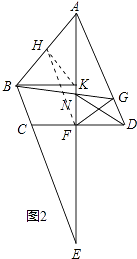
(3)如图2,延长AF、BC交于点E,过B作BK⊥AE于K,若∠BAF=2∠E,猜想,AB与KF之间有何数量关系?请说明理由.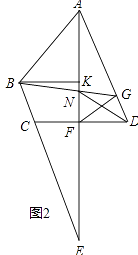
【答案】
(1)
证明:∵FG平分∠AFD,
∴∠NFG=∠GFD,
在△GFN和△GFD中, 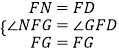 ,
,
∴△GFN≌△GFD(SAS)
(2)
证明:连接AC,如图1所示:
∵AF⊥CD,FN=FD,
∴△DFN为等腰直角三角形,
∴∠FDN=45°,
∵∠ADC=75°,
∴∠ADN=∠ADC﹣∠FDN=75°﹣45°=30°,
在Rt△AFD中,∠FAD=90°﹣75°=15°
∵AF垂直平分CD,
∴AC=AD,
∴∠ACD=∠ADC=75°,
∴∠CAD=30°,
∵AD∥BC,
∴∠BCA=∠CAD=30°,
∴∠ADN=∠BCA,
在△ADN和△ACB中, 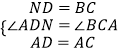 ,
,
∴△ADN≌△ACB(SAS),
∴AN=AB
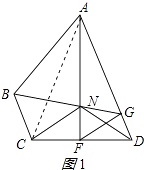
(3)
解:AB与KF之间有何数量关系为:AB=2KF;理由如下:
取AB中点H,连接HF、HK,如图2所示:
∵在Rt△AKB中,H为AB中点,
∴HK= ![]() AB=AH,
AB=AH,
∴∠HAK=∠HKA,
∵∠BAF=2∠E,
∴∠HKA=2∠E,
∵AD∥BE,
∴△AFD∽△EFC,
∴ ![]() =
= ![]() =1,
=1,
∴AF=EF,
∵H为AB中点,
∴HF为△ABE的中位线,
∴HF∥BE,
∴∠HFK=∠E,
∴∠HKA=2∠HFK,
∵∠HKA=∠HFK+∠FHK,
∴2∠HFK=∠HFK+∠FHK,
∴∠HFK=∠FHK,
∴HK=KF,
∵HK= ![]() AB,
AB,
即AB=2HK,
∴AB=2KF.
【解析】(1)由角平分线得出∠NFG=∠GFD,由SAS证明△GFN≌△GFD即可;(2)连接AC,由等腰直角三角形的性质得出∠FDN=45°,由线段垂直平分线的性质得出AC=AD,证出∠CAD=30°,由SAS证明△ADN≌△ACB,得出对应边相等即可;(3)取AB中点H,连接HF、HK,由直角三角形斜边上的中线性质得出HK= ![]() AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.
AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.