题目内容
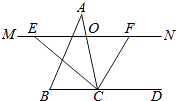
【题目】如图,在△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 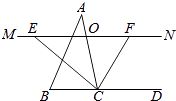
(1)求证:EO=FO;
(2)当CE=12,CF=10时,求CO的长;
(3)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
【答案】
(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF
(2)解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF= ![]() ∠ACB+
∠ACB+ ![]() ∠ACD=
∠ACD= ![]() ×180°=90°,
×180°=90°,
∴Rt△CEF中,EF= ![]() =
= ![]() =2
=2 ![]() ,
,
又∵OE=OF,
∴CO= ![]() EF=
EF= ![]()
(3)解:当O运动到AC中点时,四边形AECF是矩形,
证明:∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
由(2)可得∠ECF=90°,
∴四边形AECF是矩形.
【解析】(1)先根据等角对等边,得出OE=OC,OF=OC,再根据等量代换,得出OE=OF;(2)先根据角平分线的定义,求得∠ECF=90°,再根据勾股定理求得EF的长,最后根据直角三角形的性质,求得CO的长;(3)根据有一个角是直角的平行四边形是矩形矩形判定即可.
【考点精析】本题主要考查了直角三角形斜边上的中线和勾股定理的概念的相关知识点,需要掌握直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目