题目内容
【题目】已知:![]() ,⊙
,⊙![]() 经过点
经过点![]() 、
、![]() .以
.以![]() 为一边画平行四边形
为一边画平行四边形![]() ,另一边
,另一边![]() 经过点
经过点![]() (如图1).以点
(如图1).以点![]() 为圆心,
为圆心,![]() 为半径画弧,交线段
为半径画弧,交线段![]() 于点
于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合).
重合).
(1)求证:![]() ;
;
(2)如果⊙![]() 的半径长为
的半径长为![]() (如图2),设
(如图2),设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(3)如果⊙![]() 的半径长为
的半径长为![]() ,联结
,联结![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)![]() ,得1分,函数定义域
,得1分,函数定义域![]() ,(3)3.
,(3)3.
【解析】解决本题方法是根据题意添加辅助线,利用平行四边形的性质和全等三角形性质解题即可.
解:(1)联结![]() 、
、![]() (如图8-1),
(如图8-1),
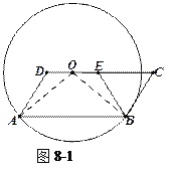
易得![]() ,
,![]() .
.
∵四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ∥
∥![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
又 ∵![]() ∥
∥![]() ,∴四边形
,∴四边形![]() 是等腰梯形.∴
是等腰梯形.∴![]() .
.
又 ∵![]() ,∴
,∴![]() .
.
即 ![]() .
.
在△AOD和△BOE中,∵![]() ,
,![]() ,
,![]() ,
,
∴△AOD≌△BOE. ∴![]() .
.
方法2:∵![]() ,
,![]() ,
,![]() ,∴△AOD≌△BOE.……
,∴△AOD≌△BOE.……
方法3:∵![]() ,
,![]() ,
,![]() ,∴△AOD≌△BOE.……
,∴△AOD≌△BOE.……
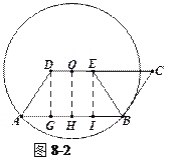
方法4:如图8-2,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .……
.……
方法5:如图8-3,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,联结
,联结![]() 、
、![]() .……
.……

(2)方法1:如图9-1,
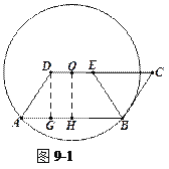
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
联结![]() ,
,![]() ,
,![]() ,得1分;得到
,得1分;得到![]() ,得2分;在Rt△ADG中,写出
,得2分;在Rt△ADG中,写出![]() ,
,![]() ,得1分;利用
,得1分;利用![]() 得到
得到![]() ,得1分,函数定义域
,得1分,函数定义域![]() ,.
,.
(3)如图10-1,
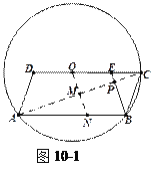
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .证明四边形
.证明四边形![]() 是平行四边形,利用
是平行四边形,利用![]() ,
,![]() 得到
得到![]() ,利用△AMN≌△CMO或
,利用△AMN≌△CMO或![]() 得到
得到![]() ,进而得到
,进而得到![]() 是
是![]() 的垂直平分线,
的垂直平分线,![]() ,利用
,利用![]() ,
,![]() 得到
得到![]() .
.
方法2.如图10-2;方法3:如图10-3;方法4(利用圆周角,略).

“点睛”本题考查了圆的综合题:熟练掌握圆心角、弧、弦、弦心距之间的关系和三角形全等的判定与性质,也考查了分类讨论的思想和勾股定理.本题时要注意一题多解的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目