题目内容
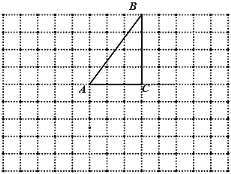
【题目】在Rt△ABC中,∠C=90°.
(1)按要求尺规作图,保留作图痕迹
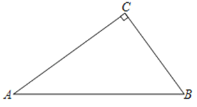
①作∠ABC平分线交AC于F点,
②作BF的垂直平分线交AB于M,以MB为半径作圆⊙M;
(2)在(1)所作图形中,证明⊙M与边AC相切;
(3)在(1)所作图形中,若∠CFB=∠CBA,BC=3,求⊙M的半径.
【答案】(1)①作图见解析;②作图见解析;(2)证明见解析;(3)![]()
【解析】
(1)①根据尺规作图过程作∠ABC平分线交AC于F点即可;②作BF的垂直平分线交AB于M,以MB为半径做⊙M即可;
②作BF的垂直平分线交AB于M,以MB为半径作圆⊙M与边AC相切;
(2)在(1)所作图形中,根据切线的判定得出FM⊥AC,即可证明⊙M与边AC相切;
(3)在(1)所作图形中,根据∠CFB=∠CBA,BC=3,角平分线的性质,求出∠A的度数,即可求⊙M的半径.
解:(1)如图所示①BF即为所求;
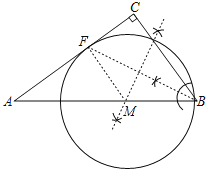
②如图所示⊙M为所求;
(2)证明:∵M在BF的垂直平分线上,
∴MF=MB,
∴∠MBF=∠MFB,
又∵BF平分∠ABC,
∴∠MBF=∠CBF,
∴∠CBF=∠MFB,
∴MF∥BC,
∵∠C=90°,
∴FM⊥AC,
∴⊙M与边AC相切;
(3)∵∠CFB=∠CBA,
∴∠A=∠CBF,
∴∠A=∠CBF=∠ABF,
∴∠A=30°,
∵BC=3,
∴AB=6,
设⊙M的半径为x,
∴MF=MB=x,则AM=2x,
∵MB+AM=AB,
∴3x=6,
∴x=2,
∴⊙M的半径为2.

【题目】为进一步提升学生的法律素质,中学组织学生开展《宪法》知识竞赛,该学校随机抽取部分学生的成绩并进行统计分析,以了解学生的法律知识水平.根据这些学生的竞赛成绩分布情况,将竞赛成绩分为甲、乙、丙、丁、戊五个等级.图表如下:
等级 | 分数/分 | 频数 | 各组总分/分 |
甲 |
| 39 | 2184 |
乙 |
| 75 | 5175 |
丙 |
| 120 | 9720 |
丁 |
|
| 4050 |
戊 |
| 21 | 2037 |

(1)求![]() 的值;
的值;
(2)竞赛成绩的中位数落在哪个等级?
(3)求这组竞赛成绩的平均值.