题目内容
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如图.
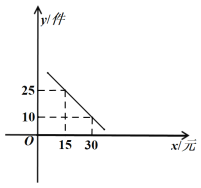
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为多少元时,此时每日的销售利润最多,最多是多少元.
【答案】(1)y=﹣x+40;(2)定为25元时,此时每日的销售利润是225元
【解析】
(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,代入(15,25),(30,10)两点,联立方程组求解即可;
(2)当每件产品的销售价定为x元时,此时每日的销售利润是w元,根据总利润=单件产品利润×销售量列出关系式,配方得出最大值即可求解.
解:(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,
![]() ,
,
解得![]() ,
,
函数表达式是y=﹣x+40;
(2)当每件产品的销售价定为x元时,此时每日的销售利润是w元;
w=(x﹣10)(﹣x+40)=-(x-25)2+225
∵a=-1<0,W有最大值,
当x=25时,w大=225
答:即当每件产品的销售价定为25元时,此时每日的销售利润是225元.

练习册系列答案
相关题目
【题目】为了提高学生身体素质,某市中小学开展阳光健步走活动,某数学兴趣小组收集了某校![]() 名学生一天行走的步数并记录如下:
名学生一天行走的步数并记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对这![]() 个数据按组距
个数据按组距![]() 进行分组,并统计整理,绘制了如下尚不完整的统计图表.
进行分组,并统计整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
组别 | 步数分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
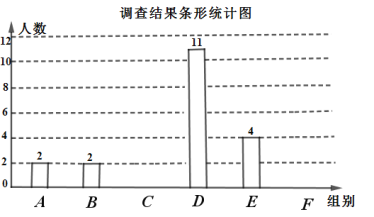
请根据以上信息,解答下列问题:
(1)填空:![]() ,
,![]()
(2)请补全条形统计图.
(3)这![]() 名学生一天行走步数的众数落在 组.
名学生一天行走步数的众数落在 组.
(4)根据科学研究,初中生一天的健步行走应不少于![]() 步,若该校有
步,若该校有![]() 名初中生,请你估计该校一天健步行走不少于
名初中生,请你估计该校一天健步行走不少于![]() 步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)