题目内容
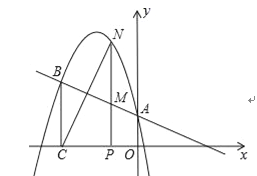
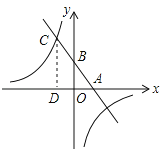
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.
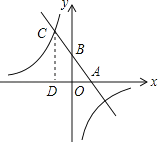
【答案】(1)y=﹣2x+6, ![]() ;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
;(2)(5,﹣4);(3)﹣2≤x<0或x≥5.
【解析】试题分析:(1)先求出A、B、C坐标,再利用待定系数法确定函数解析式.
(2)两个函数的解析式作为方程组,解方程组即可解决问题.
(3)根据图象一次函数的图象在反比例函数图象的下方,即可解决问题,注意等号.
试题解析:(1)∵OB=2OA=3OD=6,∴OB=6,OA=3,OD=2,∵CD⊥OA,∴DC∥OB,∴![]() ,∴
,∴![]() ,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴
,∴CD=10,∴点C坐标(﹣2,10),B(0,6),A(3,0),∴![]() 解得:
解得: ![]() ,∴一次函数为y=﹣2x+6.
,∴一次函数为y=﹣2x+6.
∵反比例函数![]() 经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为
经过点C(﹣2,10),∴n=﹣20,∴反比例函数解析式为![]() ;
;
(2)由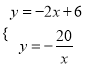 ,解得
,解得![]() 或
或![]() ,故另一个交点坐标为(5,﹣4);
,故另一个交点坐标为(5,﹣4);
(3)由图象可知![]() 的解集:﹣2≤x<0或x≥5.
的解集:﹣2≤x<0或x≥5.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目