��Ŀ����
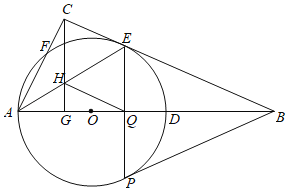
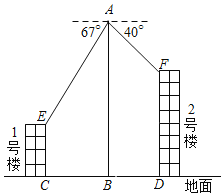
����Ŀ������ѧʵ�����ۺϿ��ϣ�ij��ȤС��ͬѧ�ú������˻���ij����С����1��2��¥���в��ʵ������ͼΪʵ��ʱ���ƵĽ���ͼ�����˻��ӵ����B��ֱ��ɵ����A�������1��¥����E�ĸ���Ϊ67�㣬���2��¥����F�ĸ���Ϊ40�㣬��ʱ�������˻��ĸ߶�Ϊ60�ף���֪1��¥�ĸ߶�Ϊ20�ף���EC��FD�ֱ�ֱ�����ڵ�C��D����BΪCD���е㣬��2��¥�ĸ߶ȣ��������ȷ��0.1�����ο�����sin40���0.64��cos40���0.77��tan40���0.84��sin67���0.92��cos67���0.39��tan67���2.36��
���𰸡�45.8��
��������
ͨ���������ߣ�����ֱ�������Σ�����ֱ�������εı߽ǹ�ϵ���ֱ����EM��AN�����������2��¥�ĸ߶�DF���ɣ�
�⣺����E��F�ֱ���EM��AB��FN��AB������ֱ�ΪM��N��
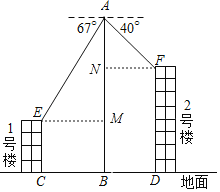
������ã�EC��20����AEM��67�㣬��AFN��40�㣬CB��DB��EM��FN��AB��60��
��AM��AB��MB��60��20��40��
��Rt��AEM��
��tan��AEM��![]() ��
��
��EM��![]() ��
��![]() ��16.9��
��16.9��
��Rt��AFN��
��tan��AFN��![]() ��
��
��AN��tan40���16.9��14.2��
��FD��NB��AB��AN��60��14.2��45.8��
��2��¥�ĸ߶�ԼΪ45.8�ף�

����Ŀ��Ϊ�����ѧ���������ʣ�ij����Сѧ��չ���⽡�����ij��ѧ��ȤС���ռ���ijУ![]() ��ѧ��һ�����ߵIJ�������¼���£�
��ѧ��һ�����ߵIJ�������¼���£�
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����![]() �����ݰ����
�����ݰ����![]() ���з��飬��ͳ�������������������в�������ͳ��ͼ����
���з��飬��ͳ�������������������в�������ͳ��ͼ����
������ͳ�Ʊ���
��� | �������� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
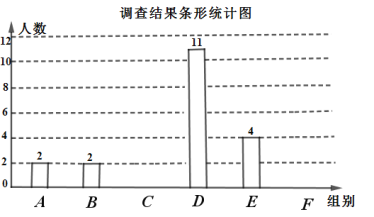
�����������Ϣ������������⣺
��1����գ�![]() ��
��![]()
��2���벹ȫ����ͳ��ͼ��
��3����![]() ��ѧ��һ�����߲������������� �飮
��ѧ��һ�����߲������������� �飮
��4�����ݿ�ѧ�о���������һ��Ľ�������Ӧ������![]() ��������У��
��������У��![]() ����������������Ƹ�Уһ�콡�����߲�����
����������������Ƹ�Уһ�콡�����߲�����![]() ����ѧ���������������������ݣ���У������������Ľ��飨�����ڽ������ߵģ�
����ѧ���������������������ݣ���У������������Ľ��飨�����ڽ������ߵģ�