题目内容
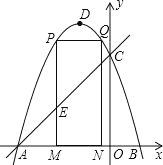
【题目】如图,抛物线y=x22x+3的图象与x轴交于A.B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A. B.C的坐标;
(2)判断以点A、C、D为顶点的三角形的形状,并说明理由;
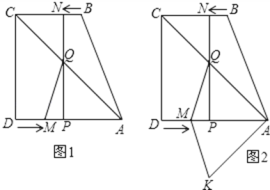
(3)点M(m,0)为线段AB上一点(点M不与点A.B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长.
【答案】(1) A(-3,0),B(1,0);(2)直角三角形;理由见解析;(3)矩形PMNQ的周长![]() .
.
【解析】
(1)通过解析式即可求出C的坐标,然后令y=0解出方程得解,即可求出A、B的坐标
(2)分求出三角形三边,会发现其满足勾股定理,所以是直角三角形
(3)根据抛物线可以得出对称轴,之后用m表示出PM以及MN的长度,之后便可求周长
(1)由抛物线![]() 可知,C(0,3)
可知,C(0,3)
令y=0,则![]()
解得:![]() 或
或![]()
∴A(-3,0),B(1,0)
(2)直角三角形
由抛物线![]() 可知,对称轴
可知,对称轴![]() ,且点D坐标为(﹣1, 4)
,且点D坐标为(﹣1, 4)
又因为点A、B、C坐标分别为(-3,0),(1,0) ,(0,3)
故根据勾股定理得:![]() ;
;![]() ;
;![]()
所以![]()
所以三角形是直角三角形
(3)由抛物线![]() 可知,对称轴
可知,对称轴![]()
∵M(m,0)
∴![]() ,
,![]()
∴矩形PMNQ的周长=2(PM+MN)=![]()
![]() .
.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目