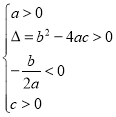题目内容
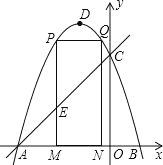
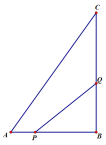
【题目】如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始向点B以1cm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,那么(1)经过几秒后,△PBQ的面积为4cm2?
(2)并通过计算回答△PBQ的面积能否达到8cm2?
【答案】(1)经过1秒后,△PBQ的面积为4![]() (2)不能,理由见解析.
(2)不能,理由见解析.
【解析】
根据题意表示出BP、BQ的长,
(1)利用三角形的面积公式列方程求解即可;
(2)利用三角形的面积公式列方程,再根据根的判别式判断方程根的情况即可.
解:根据题意,得BP=ABAP=5t,BQ=2t,
(1)设t秒后,△PBQ的面积为4cm2,
根据三角形的面积公式,得![]() BPBQ=4,即t(5t)=4,
BPBQ=4,即t(5t)=4,
整理得:t25t+4=0,
解得t=1秒或t=4秒(舍去).
答:经过1秒后,△PBQ的面积等于4cm2;
(2)△PBQ的面积不能达到8cm2,
理由:根据三角形的面积公式,得![]() BPBQ=8,即t(5t)=8,
BPBQ=8,即t(5t)=8,
整理得:t25t+8=0,
∵△=(5)24×1×8=7<0,
∴方程无实数根,
故△PBQ的面积不能达到8cm2.

【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
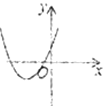
方程有两个不相等的负实根 |
|
|
____________ |
|
|
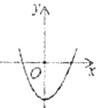
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()