Question

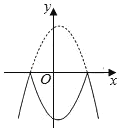
【题目】如图，将抛物线y=x2+2x+8的图象x轴上方的部分沿x轴折到x轴下方，图象的其余部分不变，得到一个新图象(实线部分)；点P(a，ka-1)在该函数上，若这样的点P恰好有3个，则k的值为_____.

Answer 1

【答案】或.

【解析】

根据题意可得，点p是直线y=kx-1上的点，直线必过（0，-1），然后根据点P个数讨论情况.

∵，当y=0时，x=-2或4，

∴抛物线与x轴的交点为（-2，0）或（4，0），

由题可得，点p是直线y=kx-1上的点，直线必过（0，-1），

当直线y=kx-1经过抛物线与x轴的交点（-2，0）或（4，0）时恰好有3个p点，

将（-2，0）代入y=kx-1得，0=-2k-1，解得，

将（4，0）代入y=kx-1得，0=4k-1，解得，

故k的值为或.