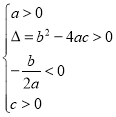题目内容
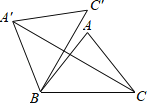
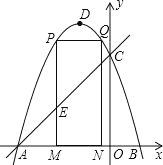
【题目】如图,正方形![]() 中,
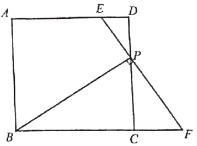
中,![]() ,P为CD边上的一点,过P点作BP的垂线交AD于点E,交BC的延长线于点F.
,P为CD边上的一点,过P点作BP的垂线交AD于点E,交BC的延长线于点F.
(1)判断线段DE、CF、CP之间的数量关系,并说明理由.
(2)若![]() ,
,![]() ,写出y与x之间的函数关系式.
,写出y与x之间的函数关系式.
【答案】(1)![]()
(2)![]()
【解析】
设CP=a,CF=b,DE=a,根据正方形与BP⊥EF得到△EDP∽△FCP∽△PCB,得到![]() ,代入即可得到a,b,c的关系,故可求解;
,代入即可得到a,b,c的关系,故可求解;
(2)根据三角形的面积公式得到![]() =
=![]() ,再根据CP与CF之间的关系即可求出函数关系式.
,再根据CP与CF之间的关系即可求出函数关系式.
设CP=a,CF=b,DE=a,
∵四边形ABCD是正方形,∴∠D=∠PCF=90°,又∠EPD=∠FPC,∴△EDP∽△FCP
∵BP⊥EF,∴∠BPC+∠CPF=90°,
又∠F+∠CPF=90°
∴∠F=∠BPC,又∠PCB=∠FCP=90°,
∴△FCP∽△PCB
故△EDP∽△FCP∽△PCB,
得到![]() ,
,
即![]()
得到
由①③得4c=4a-4b
即c=a-b,
故DE=CP-CF,
∴![]()
(2)∵y=![]() =
=![]() ,
,
∵![]() =a,
=a,
∴由①得b=![]()
代入![]() =8+2b=
=8+2b=![]()
故![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
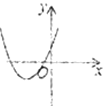
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
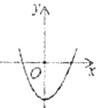
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.