题目内容
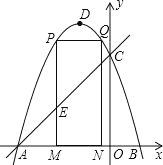
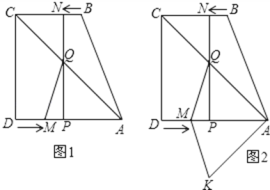
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.
(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
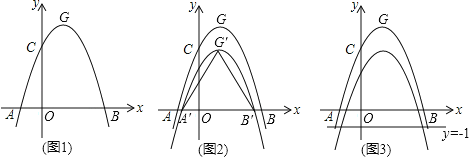
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,求 出AC的长.
【答案】(1)8﹣2t,2+t;(2)t=2;(3)![]()
【解析】
(1)由DM=2t,根据AM=AD-DM即可求出AM=8-2t;先证明四边形CNPD为矩形,得出DP=CN=6-t,则AP=AD-DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得6-t=8-(6-t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程6-t-2t=8-(6-t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=8,利用勾股定理求得AC即可.
解:(1)如图1.

∵四边形CNPD为矩形 ∴DP=CN=BC﹣BN=6﹣t,
∴AP=AD﹣DP=8﹣(6﹣t)=2+t;
故答案为:8﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴6﹣t=8﹣(6﹣t),解得t=2,
(3)①存在时刻t=1,使四边形AQMK为菱形.理由如下:
∵NP⊥AD,QP=PK
∴当PM=PA时有四边形AQMK为菱形
∴6﹣t﹣2t=8﹣(6﹣t),解得t=1,
②要使四边形AQMK为正方形.
∵∠ADC=90°,∴∠CAD=45°
∴四边形AQMK为正方形,则CD=AD,
∵AD=8,∴CD=8,
∴AC=![]() .故答案为:
.故答案为:![]()

 考前必练系列答案
考前必练系列答案